Шта је то тригонометријски круг? Чему служи тај тригонометријски круг? Сам назив тригонометријског круга нас не асоцира на тригонометрију! Да, ваша претпоставка је тачна!
Тригонометријски круг се користи за лакше дефинисање тригонометријских функција, али и директно очитавање и одређивање вредности тригонометријских функција из неких често коришћених карактеристичних углова, као што су углови са 30, 45, 60, 90, 120, 135, итд. степени.
Радијус тригонометријског круга који има дужину 1 у комбинацији са правилима за дефинисање тригонометријских функција са правоуглим троуглом служи за поједностављење начина учења и разумевања вредности тригонометријских функција углова карактеристичне величине. У наставку на овој страници објаснићемо све о тригонометријском кругу, али и много других додатних информација које су директно или индиректно везане за њега!
Све О Тригонометријски Круг
За почетак, предлажемо да добро погледате видео испод. Пажљиво размотрите све детаље у њему да бисте научили:
- Које предзнање вам је потребно да бисте разумели како да користите тригонометријски круг.
- Како дефинисати и читати вредности из тригонометријског круга.
- Како формирати табелу са најчешће коришћеним вредностима тригонометријских функција из карактеристичних углова.
Табела Вредности Добијених Тригонометријским Кругом
Ако сте пажљиво прегледали и разумели садржај горњег видео материјала, онда вероватно имате додатна питања везана за то како да добијете вредности тригонометријских функција помоћу тригонометријског круга! У овом одељку, погледајмо неколико ситуација које ћемо описати у радијанима и степенима.
Пример 1. Вредност тригонометријских функција из угла величине 30 степени!
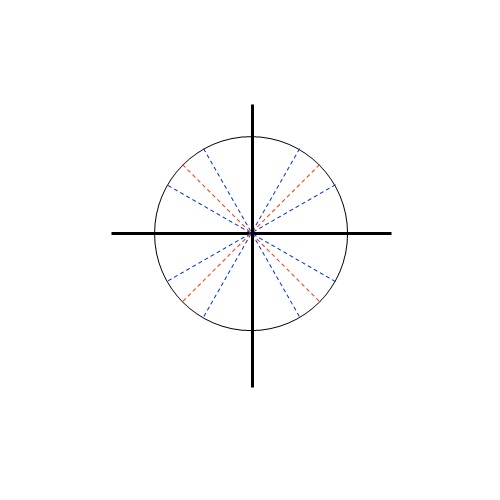
Прво, погледајмо слику која описује како се угао који је тачно 30 степени може узети у обзир коришћењем тригонометријског круга.
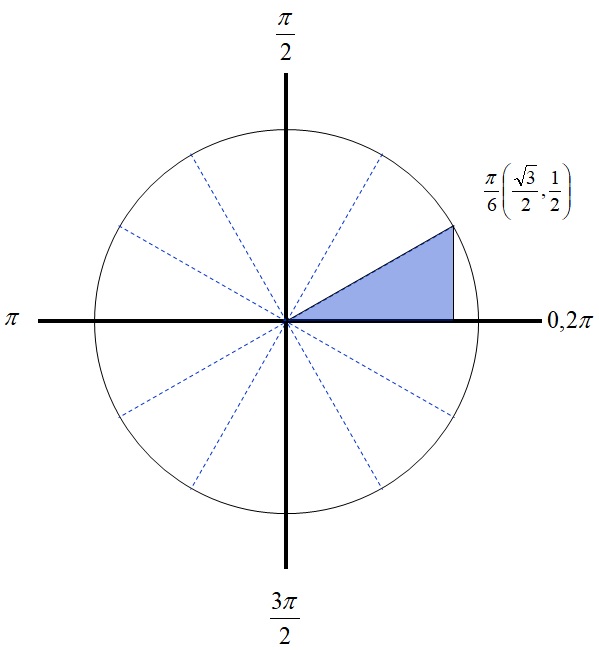
Са слике се види да су саме координате дужине два крака правоуглог троугла, док је његова хипотенуза идентична радијуса тригонометријског круга и једнака је 1. За угао од 30 степени и координата показује величину наспрамне стране, док к координата показује дужину на налегле страни. Дакле (према дефиницији тригонометријских функција), вредности тригонометријских функција за угао од 30 степени су:
Синус од 30!
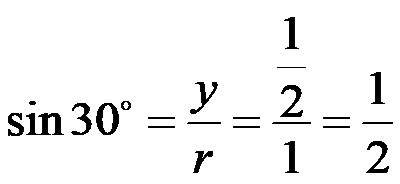
Косинус од 30!
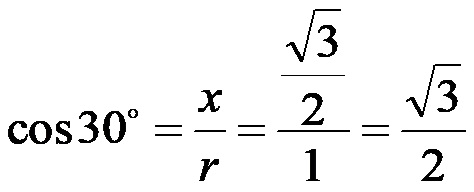
Тангенс од 30!
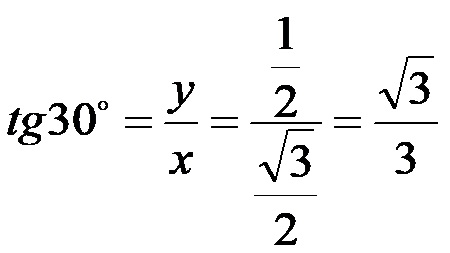
Котангенс од 30!
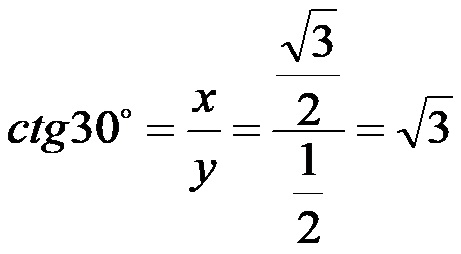
Пример 2. Вредност тригонометријских функција из угла величине 45 степени!
Прво, погледајмо слику која описује како се угао који је тачно 45 степени може узети у обзир коришћењем тригонометријског круга.
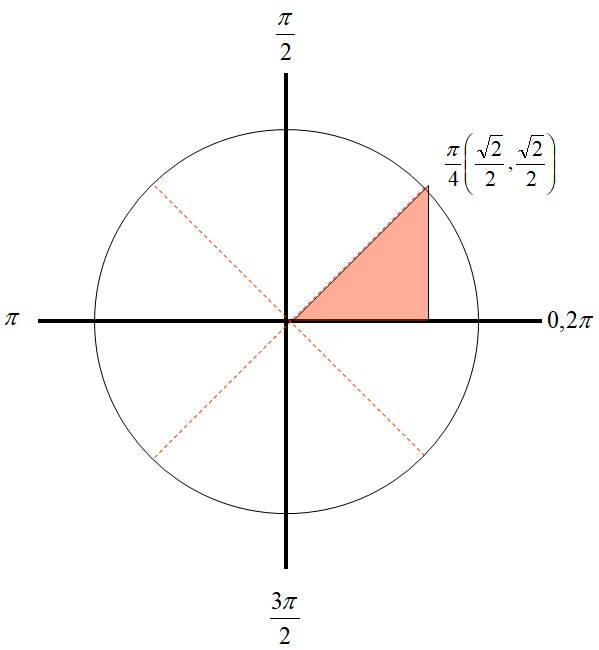
Према дефиницији тригонометријских функција и правилима која смо већ користили у претходном примеру, лако је разумети да су вредности тригонометријских функција угла од 45 степени:
Синус од 45!
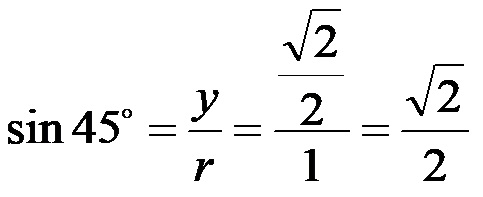
Косинус од 45!
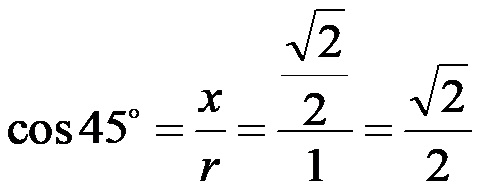
Тангенс од 45!
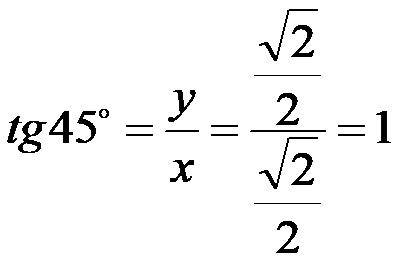
Котангенс од 45!
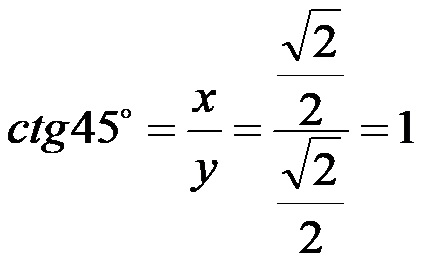
Табела Вредности
Табела испод садржи вредности тригонометријских функција карактеристичних углова добијених коришћењем тригонометријског круга!
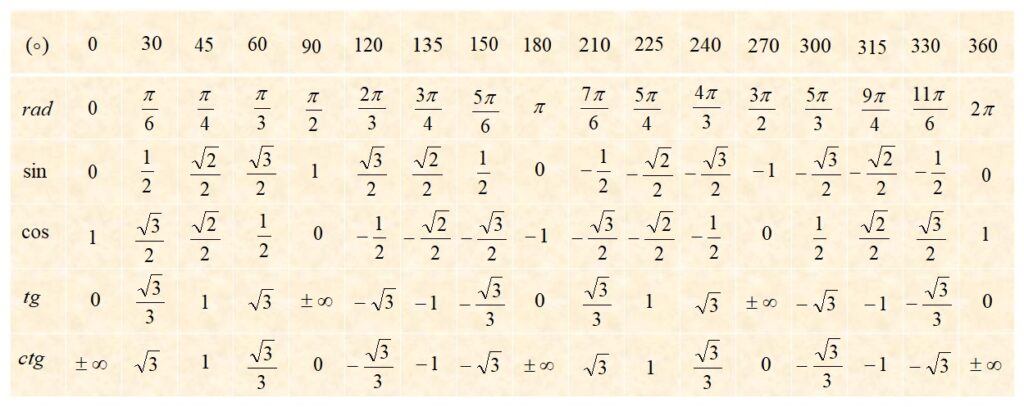
Можете користити два горња примера да упоредите резултате свих других карактеристичних углова у видеу! Једноставно, ако нешто нисте разумели први пут, предлажемо да се вратите још једном и са новим сазнањима пробате још једном и уверите се да ћете сада на исте ствари гледати на прави начин!
Tags: 120, 135, 30, 45, 60, 90, Круг, Радијани, Степен, Тригонометријски

 Сачекајте...
Сачекајте...