Тригонометријске функције и њихова дефиниција помоћу правоуглог троугла! На овој веб страници можете приступити јединственом начину дефинисања тригонометријских функција синус, косинус, тангента и котангенс помоћу правоуглог троугла. У наставку у тексту и видео снимку имате све потребне информације представљене на одговарајући начин како бисте лакше разумели овај проблем како бисте поставили добро основно знање како бисте даље разумели све тајне тригонометрије!
Корак по корак ћемо вам помоћи да разумете шта су заправо тригонометријске функције, како су дефинисане и како се користе у одређеном математичком задатку за израчунавање неких непознатих вредности у правоуглом троуглу!
Дефинисање Тригонометријске Функције
Да бисмо дефинисали четири функције изнад, користићемо правоугли троугао за његов угао који се налази на његовом теме B. Угао бета ће нам послужити да дефинишемо синус, косинус, тангенту и котангенс као основне тригонометријске функције! Испод је слика правоуглог троугла и називи његових страница у смислу како су постављене у односу на угао бета!
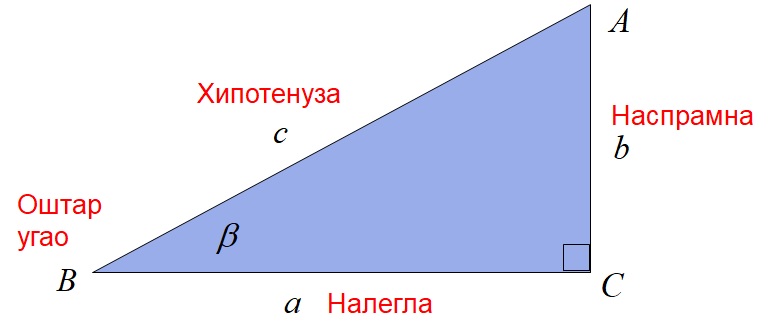
Са слике се види да се страна правоугаоника која не додирује угао бета назива “наспрамна”, док се страна која поред хипотенузе чини угао бета назива “налегла”. Ово обема странама даје посебно име у смислу њихове локације у односу на бета угао. Логично, хипотенуза (најдужа страница правоуглог троугла) задржава своје име. Управо ова имена ћемо касније користити за дефинисање тригонометријских функција синус, косинус, тангента и котангенс! Почнимо да дефинишемо тригонометријске функције за угао бета!
Синус бета је количник наспрамне катете и хипотенузе! Формула за синус бета је:
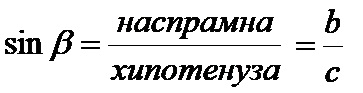
Косинус бета је количник налегле катете и хипотенузе! Формула за косинус бета је:
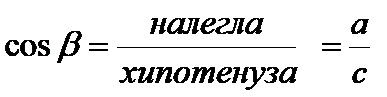
Тангенс бета је количник наспрамне катете и налегле катете! Формула за тангентну бета је:
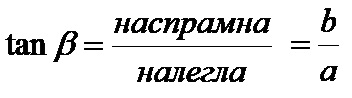
Котангенс бета је количник налегле катете и наспрамне катете! Формула за котангенс бета је:
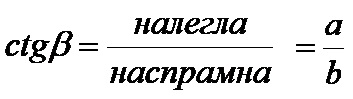
*Формуле за тригонометријске функције за угао који се налази у темену A правоуглог троугла биће потпуно другачије, јер странице правоуглог троугла у том случају треба посматрати у односу на теме A. У тој ситуацији су чланови ће имати сасвим другачије значење, тако да ће у том случају бити различите стране са наше тачке гледишта од темена B и угла бета!
Читање Тригонометријских Функција Из Правоуглог Троугла
Хајде да научимо како да читамо тригонометријске функције из правоуглог троугла чије су странице познате дужине! Погледајте пример у наставку!
Пример 1. Који разломци описују све четири тригонометријске функције за углове алфа и бета у правоуглом троуглу дате на слици испод?
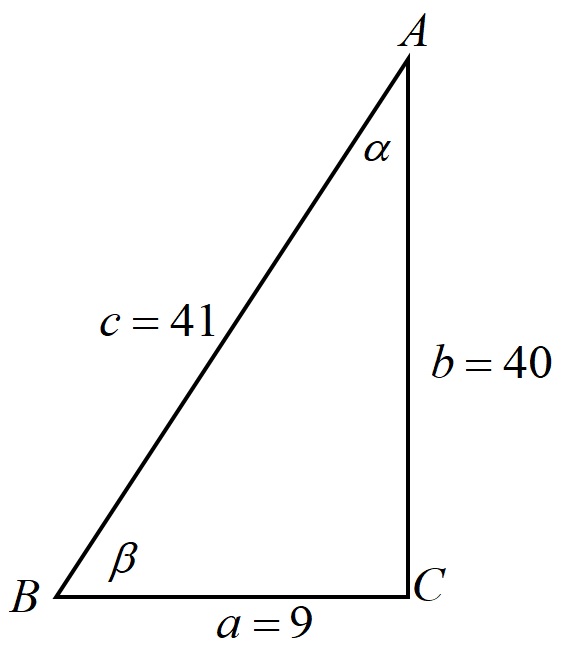
Почнимо са тригонометријским функцијама за угао алфа! За овај угао, наспрамне катете има дужину од 9cm, а налегле катете има дужину од 40cm. Знајући положај у односу на странице читамо тригонометријске функције за овај угао!
Синус алфа је количник наспрамне катете од 9cm и хипотенузе од 41cm. Формула је:
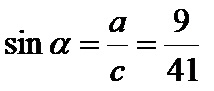
Косинус алфа је количник налегле катете од 40cm и хипотенузе од 41cm. Формула је:
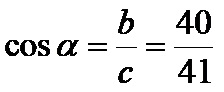
Тангента алфа је количник наспрамне катете од 9cm и налегле катете од 40cm. Формула је:
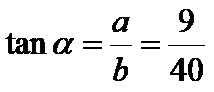
Котангенс алфа је количник налегле катете од 40cm и наспрамне катете од 9cm. Формула је:
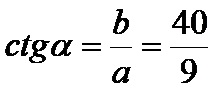
Погледајмо сада како ствари стоје у погледу бета угла! У односу на овај угао, наспрамна катета је страна која има 40cm, а налегла је катета која има 9cm! Када смо потврдили постављање страница у односу на бета угао, остаје да правилно прочитамо тригонометријске функције!
Синус бета је количник наспрамне катете од 40cm и хипотенузе од 41cm. Формула је:
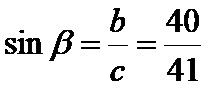
Косинус бета је количник налегле катете од 9cm и хипотенузе од 41cm. Формула је:
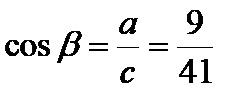
Тангента бета је количник наспрамне катете од 40cm и налегле катете од 9cm. Формула је:
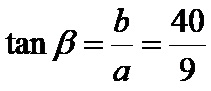
Котангенс бета је количник налегле катете од 9cm и наспрамне катете од 40cm. Формула је:
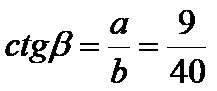
Као што се лако може видети из решеног примера изнад, уопште није тешко правилно прочитати вредности тригонометријских функција из правоуглог троугла за који су познате дужине све три његове странице.
Примена Тригонометријских Функција У Задацима
Тригонометријске функције синус, косинус, тангента и котангенс могу се применити у једноставне математичке задатке у којима се морају одредити вредности страница или углова у правоуглом троуглу. Пример математичких проблема ове врсте налази се у видеу испод! Препоручујемо да обратите пажњу на све примере у видеу јер ти примери могу помоћи да научите много!
Тригонометријске функције су проблематичан део математике за многе ученике и људе уопште. Ако вам је потребна додатна помоћ или појашњење, слободно напишите свој захтев у коментару испод или путем е-поште. Покушаћемо да вам помогнемо!
Tags: Косинус, Котангенс, Правоугли, Синус, Тангенс, Тригонометријске, Троугао, Формула, Функције

 Сачекајте...
Сачекајте...