Транслација је врста геометријске трансформације која се може користити за преношење тачке, сегмента, линије или геометријске фигуре са једне локације на другу уз придржавање одређеног строго дефинисаног правила! Приликом сваког транслације треба да се побрине да се сви тачке (ако их има више) пренесу по истом правилу. Резултујућа тачка након преноса са транслација је слика оригиналне тачке одакле смо започели пренос. Логично, ако транслацијом пренесемо сегмент, права или геометријску фигуру, онда је опет почетно стање оригинал, а коначна слика тог оригинала.
Како Се Врши Транслација У Равни
Да би се транслација успешно завршила, мора постојати исправно дефинисано правило. Ако се транслација треба извршити под углом, онда треба да буду доступни подаци за величину тог угла.
Најједноставнији метод за транслацију у карактеристичним правцима је коришћење правца као што су десно, лево, горе или доле! Исти поступак би био и ако се транслација врши у координатном систему, с том разликом што се у координатном систему користе знаци + и -, па у односу на коју се тачно координату ради, треба извући закључак где је да носе ту тачку, сегмент, права или геометријску фигуру. У сваком случају овакву врсту транслације као геометријске трансформације у координатном систему врло је лако завршити!
Размотримо две такве ситуације у којима постоји потреба да се геометријска фигура транслатирају у координатни систем.
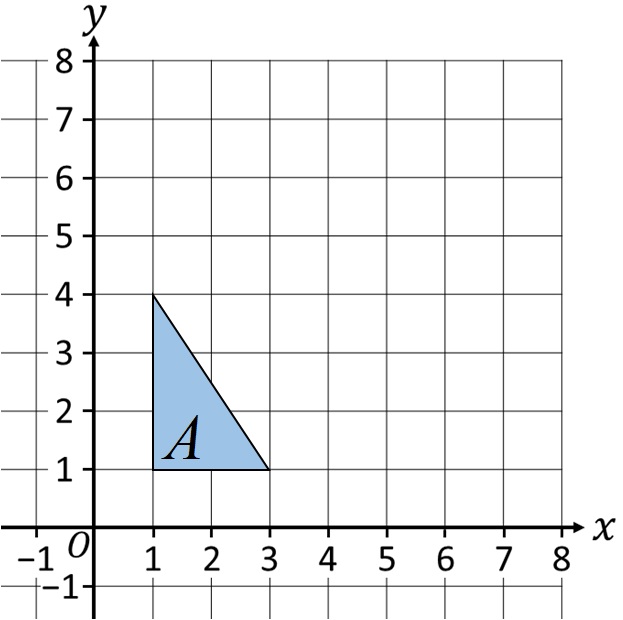
Пример 1. Конструишите транслацију геометријске фигуре A у координатни систем за +4 у односу на осу x!
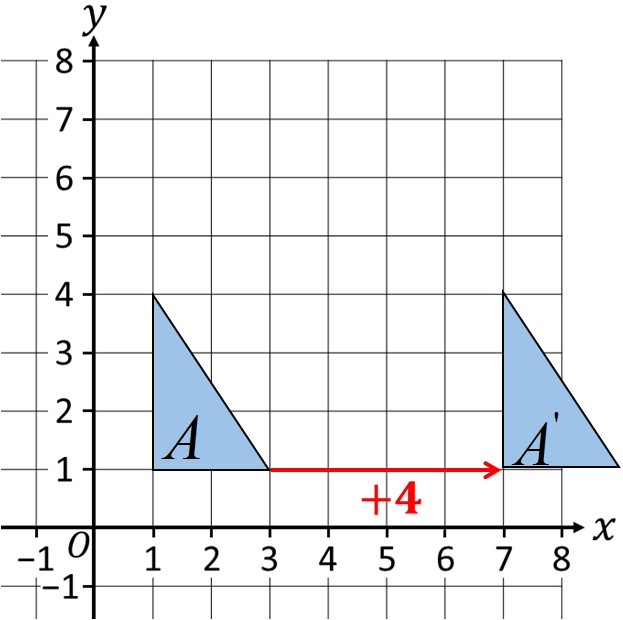
Транслацију треба извршити за +4 у односу на x-осу! То значи да сваки теме геометријске фигуре треба да буде транслатиран удесно за четири места! Све би требао изгледати као на слици испод!
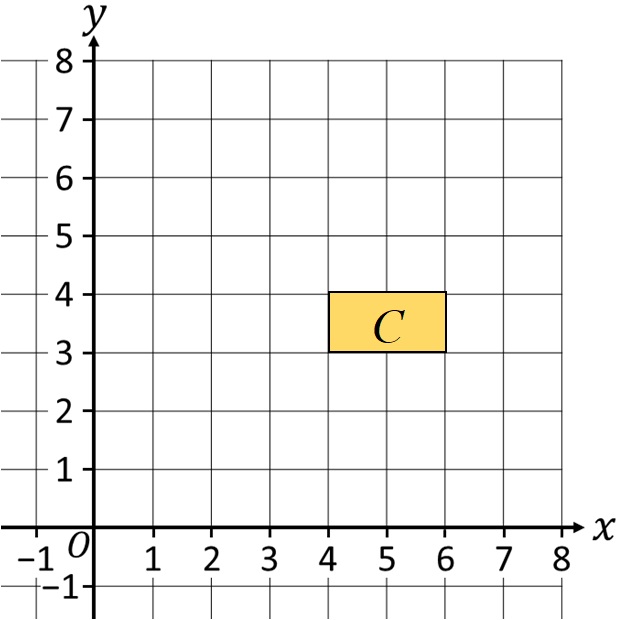
Пример 2. Конструишите транслацију геометријске фигуре C дате на доњој слици у координатни систем за -2 у односу на x-осу и +3 у односу на y-осу!
Прво хајде да завршимо транслацију у односу на x осу! У овом случају, пошто морамо транслатирати за -2, то значи да сваку тачку фигуре треба да померимо улево дуж хоризонталне линије паралелне са самом x-осом. За овај пример би требало да изгледа као на слици испод!
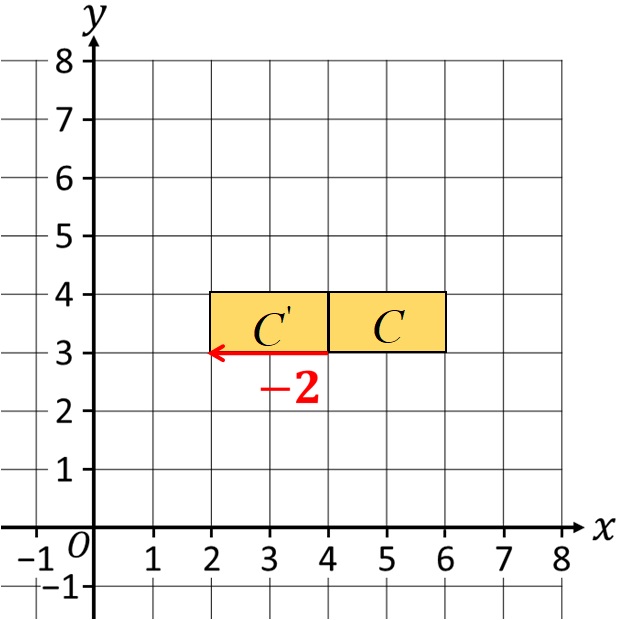
Чим је први део завршен, са места где смо добили локацију геометријске фигуре након транслацију, остаје да је померимо за три места навише дуж праве паралелне са y осом. Комплетно решење је дато на слици испод!
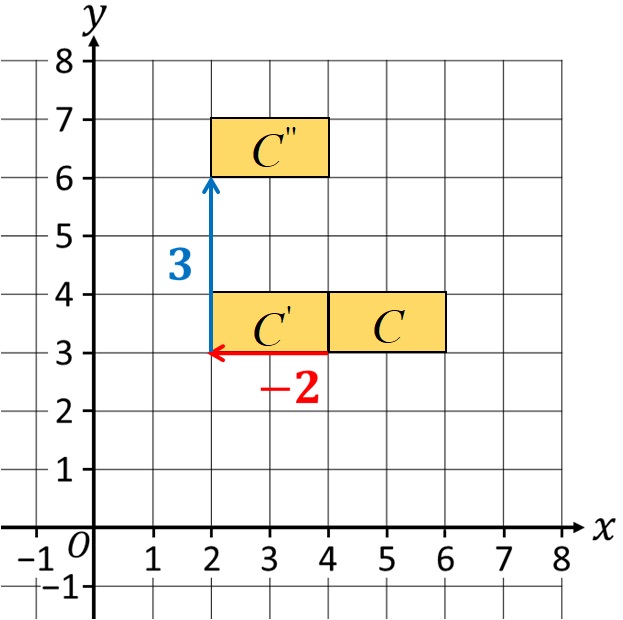
Као што се лако може видети, транслација је веома лако завршити у координатном систему!
Видео
Видео материјал који вам је доступан кликом испод садржи много примера са транслација геометријских фигура у координатни систем, али и анализу многих датих комплетних вежбе транслације како би гледаоци препознали правило по коме је правило транслација упоређивано. Ове вежбе су изузетно важне за правилан развој логичког мишљења.
Tags: Координатни, Систем, Транслација

 Сачекајте...
Сачекајте...