Скраћивање разломака код множења је поступак који је веома лак и веома користан како би множење тих разломака било што једноставније. Овај поступак нам омогућава да завршимо скраћивање разломака на почетку поступка уместо да то радимо на крају математичке операције. У наставку у овом тексту ћемо вам показати како да скраћујете разломке приликом множења пре него што почнете да множите! Испод су правила која треба да се придржавате, као и релевантни примери где се ова правила користе.
Правила За Скраћивање Разломака Код Множења
Правила за скраћивање разломака код множења су врло једноставна. Две правила су:
- Прво уочавамо бројилац првог разломка (први множилац) и именилац другог разломка (други множилац). Ако имају заједничке делиоце, делимо их њиховим највећим заједничким делиоцем. Бројеви које смо добили као резултат поделе остају на свом месту.
- Затим налазимо именилац првог разломка (први множилац) и бројилац другог разломка (други множилац). Ако имају заједничке делиоце, делимо их њиховим највећим заједничким делиоцем и на њиховом месту остају бројеви које смо добили као резултат дељења.
Наравно, скраћивање разломака код множења је могуће само ако одговарајући парови бројева које смо описали у горњим правилима имају заједничке делиоце. Ако ови парови бројева немају ниједан заједнички делилац, онда скраћивање разломака при множењу није могуће!
Примери Скраћивања Разломака Код Множења
Сада је на нама ред да применимо правила за скраћивање разломака код множења. Погледајмо два примера!
Пример 1. Извршите скраћивање разломака датих на слици испод пре него што их помножите!
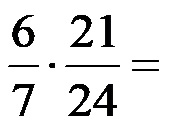
Бројеви 6 и 24 имају највећи заједнички делилац – број 6. Дакле, оба броја делимо са 6. Бројеви 7 и 21 имају највећи заједнички делилац број 7, па оба броја делимо са 7. После скраћивања добијамо следеће израз:
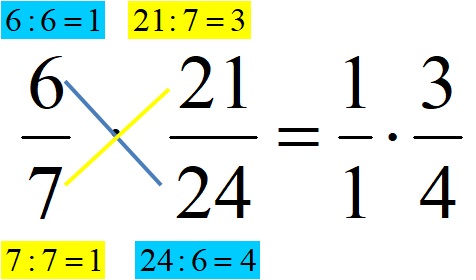
Коначно, можемо на лакши начин израчунати производ два разломка. Прорачун је дат на слици испод!
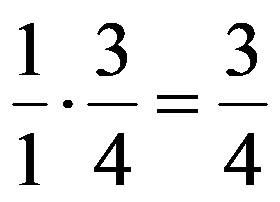
Пример 2. Извршите скраћивање разломака датих на слици испод пре него што их помножите!
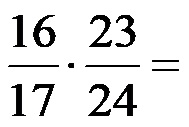
Бројеви 16 и 24 имају највећи заједнички делилац – број 8. Дакле, бројеве 16 и 24 делимо бројем 8. Бројеви 17 и 23 немају један заједнички делилац, па не можемо да поједноставимо овај пар. Након скраћивања једног од парова бројева добија се следећи израз.
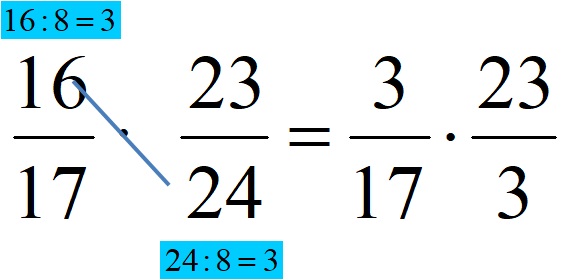
Коначно множење би требало да изгледа овако:
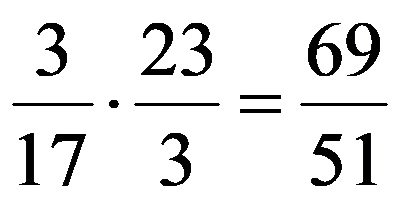
Видео Примери
Многи додатни примери математичких проблема који користе скраћивање разломака код множења доступни су само једним кликом испод. Погледајте примере како бисте стекли навику решавања математичких задатака овог типа!
Хвала на времену! Сваки читалац је добродошао да затражи одређени садржај који тренутно није на нашем сајту, а који бисмо желели да имамо. Слободно поделите свој упит у коментару испод!
Tags: Множења, Множење, Правило, Пример, Разломака, Скраћивање

 Сачекајте...
Сачекајте...