Овај пост је о синусна теорема – једној од најважнијих теорема у тригонометрији. Ова теорема омогућава да се користи њена примена за израчунавање дужине странице било ког троугла, или величине углова троуглова. Зато ћемо у данашњем посту добро објаснити шта је синусна теорема и како се примењује на конкретним примерима и математичким задацима. Сама страница има видео водич на дну који врло јасно показује како је синусна теорема дефинисана за различите троуглове.
Како Је Дефинисана Синусна Теорема
Да бисмо извели закључак који називамо синусна теорема, један троугао треба поделити на два правоугла троугла спуштањем једне од три висине. Дужина висине је заједничка страница за оба различита правоугла троугла. Његова дужина се изражава кроз чланове и првог и другог троугла, па пошто оба израза имају идентичан резултат, можемо их међусобно изједначити. Овако је дефинисана. Погледајте слику испод и приметите како се један троугао дели на два правоугла троугла спуштањем једне од висина!
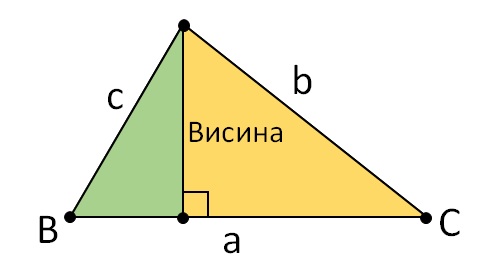
За зелени троугао са горње слике можемо написати следеће формуле:
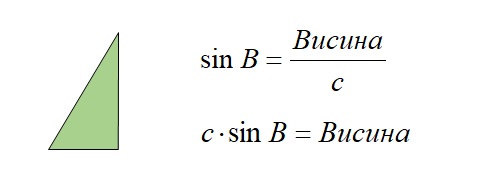
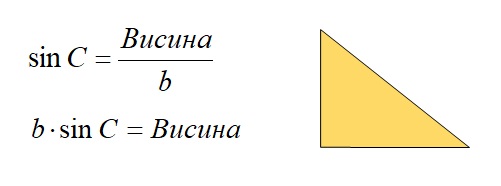
На исти начин, следеће формуле се могу извести за наранџасти троугао:
Логично, пошто су обе формуле (из зеленог и из наранџастог троугла) једнаке дужини висине, можемо записати да између њих постоји једнакост. Формула се примењује:
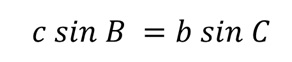
Одакле лако можемо извести закључак за први део синусна теорема:

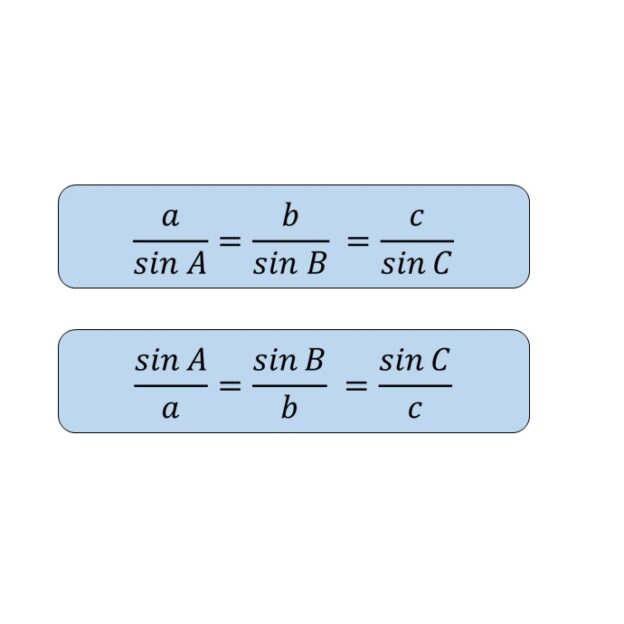
Ако овај поступак поновимо спуштањем све три висине на исти начин, добићемо цео садржај теореме синуса која гласи:
Примена На Синусна Теорема
Примена је огромна! Ова теорема је једна од најчешће коришћених теорема у тригонометрији, геометрији и математици уопште. Главна примена теореме о синусима односи се на одређивање дужине странице која има непознату дужину, односно величине угла у троуглу чију величину не знамо.
У наставку имате прилику да размотрите пример израчунавања дужине странице троугла и величине угла помоћу теореме синуса.
Пример 1. Израчунај колико је дуга страница х троугла на слици испод!
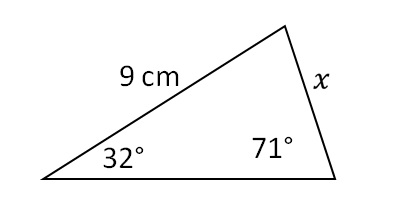
Из датих података на горњој слици може се лако разумети да имамо довољно података да применимо синусна теорема. Однос који треба да успоставимо је:
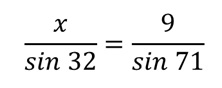
Из чега следи да:
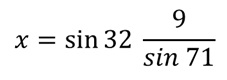
Израчунавањем вредности тригонометријских функција добија се коначни резултат који се односи на дужину непознате странице троугла:
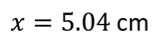
Пример 2. Израчунај величину угла х у троуглу на слици испод!
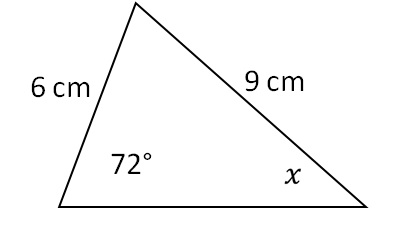
Примењујући синусна теорема, записујемо релацију:
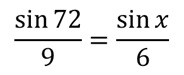
Из чега следи да:
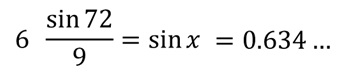
Да бисмо коначно лако утврдили да је величина непознатог угла:
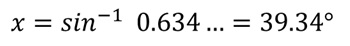
Видео Докази И Примери
Видео материјал који вам је доступан само једним кликом испод садржи доказ како је теорема дефинисана за неколико различитих троуглова. Такође у видеу можете видети огроман број решених примера у којима се дужина страница различитих троуглова или величина њихових углова одређује помоћу теореме синуса! Препоручујемо вам да прегледате што више примера!

 Сачекајте...
Сачекајте...