Сабирање разломака са различитим имениоцима је најпроблематичнији математички поступак у основном образовању. Да ли сте спремни да прихватите изазов учења сабирања разломака са различитим имениоцима? Ако сте спремни, ово је право место да то урадите на најлакши начин.
Наш водич садржи много корисних информација и решених примера који ће вам помоћи у процесу учења! Требало би да знате од самог почетка да ће сваки ученик који успешно прође ову математичку препреку сигурно моћи да се снађе у будућности када изучава теже математичке изазове. Кроз овај поступак покушаћемо да започнемо први најважнији корак да постанемо бољи математичари.
Правило За Сабирање Разломака Са Различитим Имениоцима
Све у математици је лакше ако се придржавате одређеног правила да бисте успешно извршили математички поступак. За сабирање разломака са различитим имениоцима направили смо правило које можете видети испод!
- Прво одреди најмањи заједнички именилац различитих именилаца разломака који се сабирају.
- Проширите све разломке тако да у имениоцу садрже најмањи заједнички именилац који сте одредили у првом кораку.
- Примените правило са истим имениоцима јер су разломци које добијете у другом кораку разломци који већ имају исте имениоце.
Цео поступак сабирања разломака са различитим имениоцима своди се на поштовање три горе наведена правила. Ако се тачно придржавате правила, готово је немогуће погрешити у прорачуну. Како користимо ова правила при решавању конкретних примера сабирања разломака са различитим имениоцима погледајте у наставку овог текста!
Примери Сабирања Разломака Са Различитим Имениоцима
Испод на овој страници можете видети два потпуно решена примера сабирања разломака са различитим имениоцима. Сваки од три корака је у њима примењен и потпуно објашњен. Препоручујемо да пажљиво проучите ова два примера пре него што почнете да их сами решавате!
Пример 1: Сакупите разломке дате на слици испод!
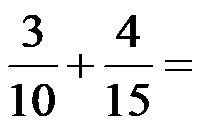
Разломци дати на горњој слици имају имениоце 10 и 15. Почнимо да примењујемо горња правила!
Први корак: Прво морате да одредите НЗС именилаца 10 и 15. Кликните овде ако вам треба подсетник како да одредите НЗС за два или више бројева. Најмањи заједнички именилац бројева 10 и 15 је:
НЗС (10,15) = 30
Други корак: Пошто већ знамо да је НЗС за различите имениоце број 30, проширујемо разломке тако да након проширења оба треба да имају именилац 30.
Након проширења, разломак 3/10 би требао изгледати овако:
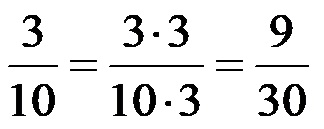
Након проширења, разломак 4/15 би требао изгледати овако:
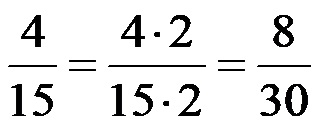
Са проширењем смо заправо извршили трансформацију из разломака са различитим имениоцима у разломке са истим имениоцима! Цео израз након трансформације изгледа овако:
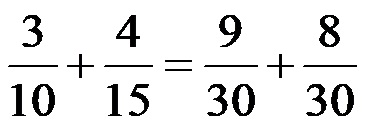
Трећи корак: Коначно, морамо да саберемо разломке који већ имају исте имениоце. Коначна акција је веома лака!
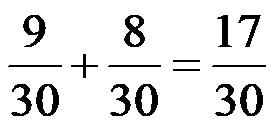
Збир разломака 3/10 и 4/15 је разломак 17/30!
Сигурно ћете се сложити да када систематски применимо сва три корака правила за сабирање разломака са различитим имениоцима, онда је цело решење ове врсте задатка много лакше!
Пример Сабирања 3 Разломка Са Различитим Имениоцима
У другом примеру испод, решићемо математички задатак у коме треба додати три разломка који имају различите имениоце. Правила остају иста без обзира да ли треба да саберете два, три или више разломака! Погледајте како важе иста правила када треба додати три разломка са различитим имениоцима!
Пример 2: Сакупите разломке дате на слици испод!
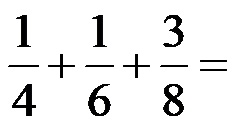
Разломци на горњој слици имају имениоце 4, 6 и 8. Почињемо применом три корака!
Први корак: На почетку се мора одредити НЗС за имениоце 4, 6 и 8. Најмањи заједнички именилац за бројеве 4, 6 и 8 је:
НЗС (4,6,8) = 24
Други корак: Проширујемо све три разломке на разломке који имају имениоце 24!
Након проширења, разломак 1/4 би требао изгледати овако:
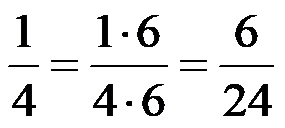
Исто, разломак 1/6 би требао изгледати овако:
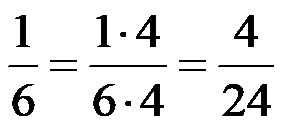
Након проширења, разломак 3/8 би требао изгледати овако:
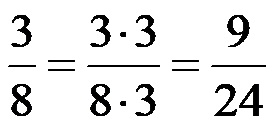
Трансформација три разломка са различитим имениоцима у разломке са истим имениоцима! Цео израз након трансформације изгледа овако:
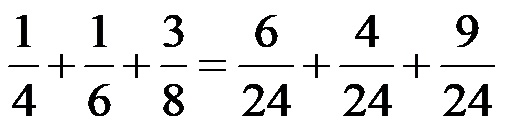
Трећи корак: Коначно, морамо да саберемо три разломка који већ имају исте имениоце.
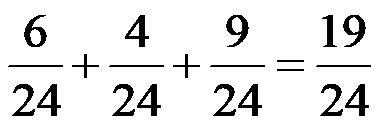
Видео
Препоручујемо вам да погледате видео испод како бисте лакше савладали математичку вештину сабирања разломака са различитим имениоцима! Видео садржи много примера који ће вам помоћи да аутоматизујете коришћење три правила која смо већ применили у два решена примера изнад на овој страници.
Радни Листови
Ако желите сами да решите неке примере, онда сте добродошли да преузмете наше радне листове који садрже примере сабирања разломака са различитим имениоцима. Наш Ворд документ садржи одељак у којем можете самостално креирати сопствене примере који се односе на исти математички проблем. Нагласите ову математичку методологију ако желите да постигнете највиши ниво знања!
Tags: Имениоцима, Примери, Различитим, Разломака, Са Различитим, Сабирање

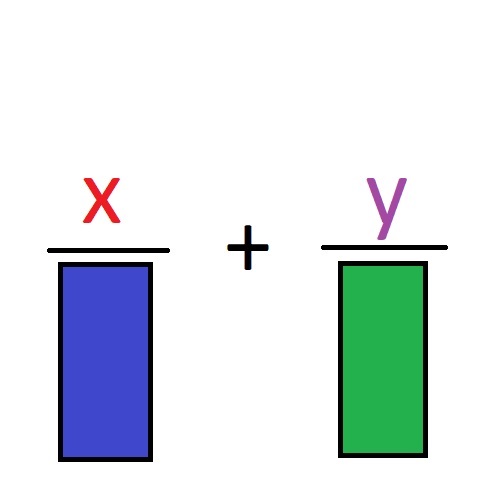
 Сачекајте...
Сачекајте...