Данашња лекција садржи туторијал о сабирању и одузимању полинома! Шта ја сабирање и одузимање полинома? Овде на овој страници можете видети како сабирати и одузимати полиноме користећи две различите методе. Истовремено, сваком читаоцу је доступно много примера који имају целовито решење. Неки од тих примера се могу прочитати директно на овој страници испод, док је већина њих доступна у видео формату у видеу на дну.
Како Сабирати И Одузимати Полиноме
Сабирање и одузимање полинома уопште није тешка математичка операција ако се уради тачна и детаљна анализа различитих делова сваког од полинома које сабирамо или одузимамо! Приликом сабирања и одузимања полинома важи да су ове математичке операције изводљиве само за оне чланове у полиномима који су међусобно повезани, односно имају исту основу, односно исти променљиви део!
Пре него што одлучите да сабирате или одузмете полиноме, прво размотрите све њихове чланове и откријте који су од њих међусобно повезани. Да би се смањиле шансе за грешку при извршавању ове две математичке операције, лепо је направити правилно груписање повезаних делова приликом њиховог извођења. Због тога се у пракси користе две различите методе сабирања и одузимања полинома, које се разликују према начину груписања различитих делова полинома. Ове методе се називају хоризонтална и вертикална метода. Ако групишемо чланове у хоризонталну линију онда користимо хоризонталну методу, док ако је груписање урађено у вертикалној линији онда користимо вертикалну методу.
У наставку можете видети како се ови математички проблеми решавају коришћењем хоризонталне и вертикалне методе!
Примери Сабирања И Одузимања Полинома
Први пример испод описује хоризонтални метод сабирања и одузимања полинома! Размотрите решење веома пажљиво!
Хоризонтална Метода За Собирање И Одузимање Полинома
Пример 1. Израчунајте збир полинома на слици испод!
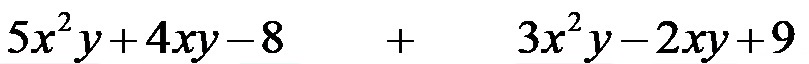
У првом кораку нећемо мењати полиноме осим што ћемо подвући повезане појмове линијама у различитим бојама да бисмо открили који члан полинома треба да сабирамо. Правилна анализа би требала изгледати овако:
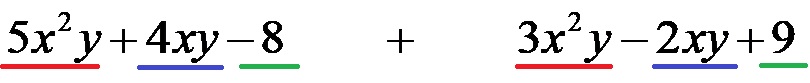
Неки чак групишу повезане чланове у заградама како би додатно смањили шансе за прављење одређене грешке. Ово уопште није обавезно, али многи се осећају сигурније када су сродни чланови јасно груписани. Један тип таквог груписања је дат на слици испод!
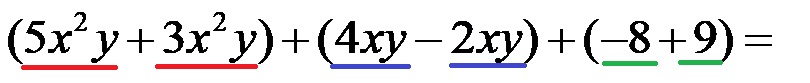
Без обзира за који тип груписања се одлучите, на крају сваки пар сродних чланова сабирамо један другом! Ако неки члан нема свој одговарајући члан у другом полиному, само га преписујемо у збир без икаквих промена. Збир полинома би требало да изгледа овако:
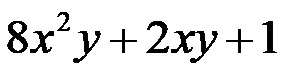
Вертикални Метода За Собирање И Одузимање Полинома
Следећи пример описује како се користи вертикални метод за сабирање и одузимање полинома!
Пример 2. Израчунај разлику полинома датих на слици испод!
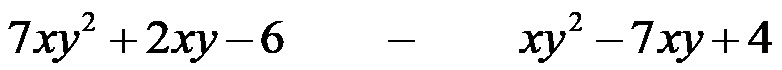
Прво мењамо знак који се налази између полинома са + и истовремено мењамо све предзнаке у другом полиному. Тако трансформишемо одузимање полинома у сабирање полинома!
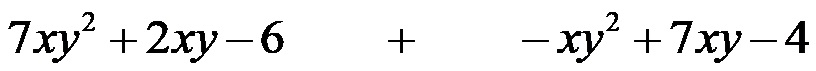
Онда, подвлачећи, урадимо анализу ко су сродни чланови!
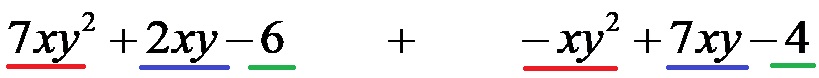
У следећем кораку можете јасно видети како се хоризонтална и вертикална метода разликују. Овде, када користимо вертикалну методу, довршавамо груписање постављајући повезане чланове полинома један испод другог. Исправно груписање при решавању другог примера требало би да изгледа овако:
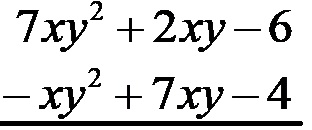
На крају само израчунамо разлику између повезаних чланова, а они који немају одговарајући сродни члан се преписују у резултат без икаквих промена.
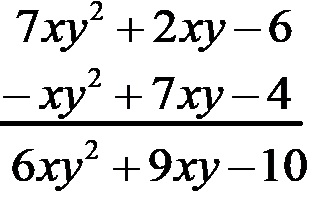
Видео Примери
Видео испод има тоне решених примера са сабирањем и одузимањем полинома! У многим ситуацијама се у различитим полиномима користи другачија методологија груписања сродних појмова, што вам даје изузетну шансу да научите много док гледате видео.
Ако неко од вас има неко додатно питање, пошаљите нам то питање! То можете у коментарима или мејлом и ми ћемо се потрудити да вам одговоримо у најкраћем могућем року. Хвала вам што сте своју страст за учењем математике поделили са нама!
Tags: Одузимање, Полинома, Пример, Сабирање, Сабирање И Одузимање

 Сачекајте...
Сачекајте...