Сабирање и одузимање корена на прави начин! Овде ћете видети како сабирате и одузимате корене, много примера и решених задатака! Најважнија процедура везана за ове математичке операције са коренима је да свако треба да буде у стању да изврши одговарајуће поједностављење корена (само ако је могуће), како би разумео да ли се дати корени уопште могу сабирати или одузимати.
Сама процедура сабирања и одузимања корена је веома лака, проблематичнији део је разумети да ли дати корени имају или немају исти коренски израз. Закључак је следећи: Сабирање и одузимање корена могуће је само ако два (или ако сакупимо више корена) корена имају идентичан коренски израз. Ако је њихов коренски израз различит, онда се корена уопште не могу сабирати и одузимати!
Правила Сабирање И Одузимање Корена
Сабирање и одузимање корена своди се на сабирање и одузимање множитеља који долазе пре коренског израза. При томе, једноставно, коренски израз остаје исти (уопште га не мењамо), а математичке операције важе само за множитеље. Ако саберемо корене, онда израчунамо њихов збир, а ако их одузмемо, израчунамо њихову разлику.
Сабирање Корена
Хајде да прво видимо два примера са сабирањем корена!
Пример 1. Израчунајте збир корена на слици испод!
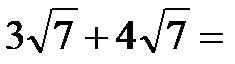
Као што смо већ поменули у тексту, коренски израз остаје непромењен, а множитељи који се налазе испред корена се додају! Дакле, збир корена је:
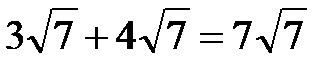
Пример 2. Израчунајте збир корена на слици испод!
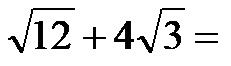
Очигледно, на први поглед, коренски израз корена је другачији, или се барем тако чини. У овим ситуацијама, морамо открити да ли се један или оба корена могу упростити, да схватимо да ли их уопште можемо сабирати или не! Број 12 можемо представити као производ између бројева 4 и 3, а пошто је корен од 4 број 2, можемо извући 2 испред корена као множилац, док ће испод корена остати само број 3.
У тој ситуацији, након упрошћавања првог корена, може се видети да оба корена имају исти коренски израз. Сада је лако схватити да можемо сабрати корење. Целокупно решење је дато на слици испод!
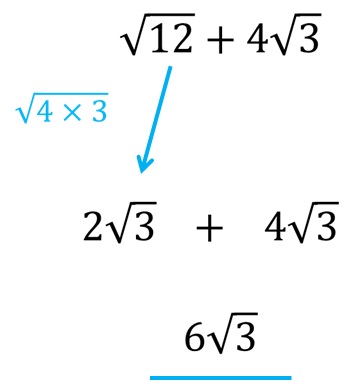
Одузимање Корена
Сада је ред да видимо два примера са одузимање корена!
Пример 3. Израчунај разлику између корена датих на слици испод!
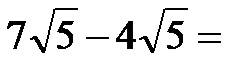
Очигледно је да корени на горњој слици имају исти коренски израз, тако да их је врло једноставно одузети један од другог. Једноставно речено, коренски израз остаје непромењен, док одузимамо множитеље. Лако је видети да је решење:
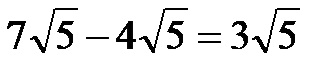
Пример 4. Израчунајте разлику између корена слике испод!
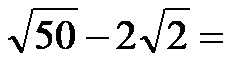
Опет, баш као у другом примеру изнад, немамо јасну представу да ли корени на горњој слици имају исте коренске изразе или не. Прво покушавамо да поједноставимо!
Број 50 можемо представити као производ између бројева 25 и 2, а пошто је корен од 25 број 5, можемо извући 5 испред корена као множилац, док ће испод корена остати само број 2. Сада је већ јасно да ова два корена имају исти израз корена и можемо их одузети.
Цео поступак одређивања разлике између два корена је дат на слици испод!
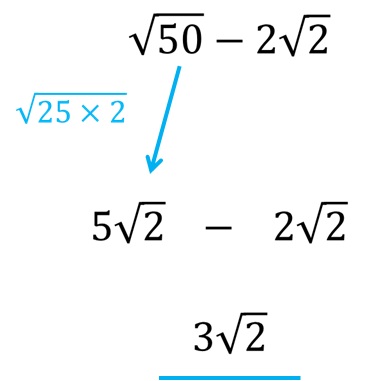
Видео Примери
Дозволите себи да утонете у разне примере садржане у видеу испод! Обиље примера са сабирањем и одузимањем корена помоћи ће вам да научите многе математичке трикове у потрази за решењем. Препоручујемо да их све проверите!
Tags: Задаци, Корена, Одузимање, Пример, Сабирање, Сабирање И Одузимање

 Сачекајте...
Сачекајте...