Шта је растављање на просте чиниоце? У овом тексту можете видети приказ растављање простих чинилаца бројева од 1 до 100! Иако је поступак на први поглед веома једноставан, поступак је изузетно важан. Ако га правилно користите у будућности, помоћи ће вам да лакше научите много сложеније математичке вештине! Ако знате да правилно растављање број на његове просте чиниоце, онда ћете сигурно моћи да решавате сложеније математичке проблеме користећи математичке трикове. Погледајте наш текстуални садржај у наставку!
- Правило за дељење броја на просте чиниоце.
- Много примера са дељењем коришћењем грана чиниоце.
- Табела простих чинилаца бројева од 1 до 100.
- Много видео примера осмишљених да вам олакшају прилагођавање растављање на просте чиниоце.
Почињемо са:
Правило За Растављање На Просте Чиниоце
Логично, на почетку, пре него што се приступи практичној растављање на просте чиниоце, потребно је дефинисати шта је прост, а шта комплексан број! Хајде да прво урадимо управо то!
- Прост број је сваки број који је дељив само сам са собом и бројем 1 без остатка. Када делите прост број са другим бројем, увек добијате остатак!
- Сложени број је сваки број који је дељив са 1, самим собом и најмање још једним бројем без остатка.
Главни предуслов за почетак поступка је задовољен. Када се већ добро зна шта је прост број, а шта сложени број, можемо дефинисати правило за растављање на просте чиниоце. Урађено је одмах испод!
Број се може раставља на различите чиниоци све док сви његови чиниоци нису у облику простих бројева. При томе, уопште није важно по ком тачно правилу ће се раставњање извршити. Потребно је само да раставњамо сваки различит чиниоци док их све не доведемо до простог броја.
У наставку можете видети неке конкретне примере у којима се врши растављање!
Примери
Пример 1: Број 10 на просте чиниоце!
Ако почнемо да растављамо број 10, лако је видети да га је најједноставније представити као производ бројева 2 и 5. Бројеви 2 и 5 су прости бројеви, па је растављање одмах завршено. Графички, растављање броја 10 је представљено на слици испод!
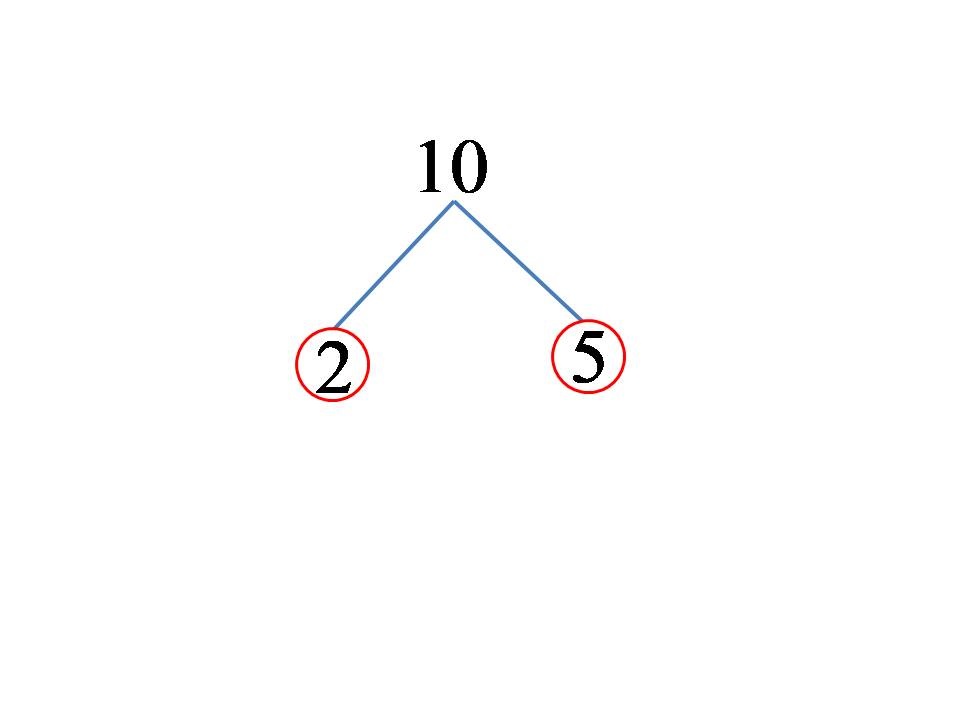
Број 10, након што се растављи на просте чиниоце, може се написати у следећем облику:
10 = 2 x 5
Пример 2: Број 12 на просте чиниоце!
Почнимо да растављамо број 12! Једна од могућности је да га растављамо на производ бројева 3 и 4. Број 3 је прост, али сложени број 4 треба да наставимо да га растављамо. Растављамо 4 на производ бројева 2 и 2. Графички је декомпозиција броја 12 представљена на слици испод!
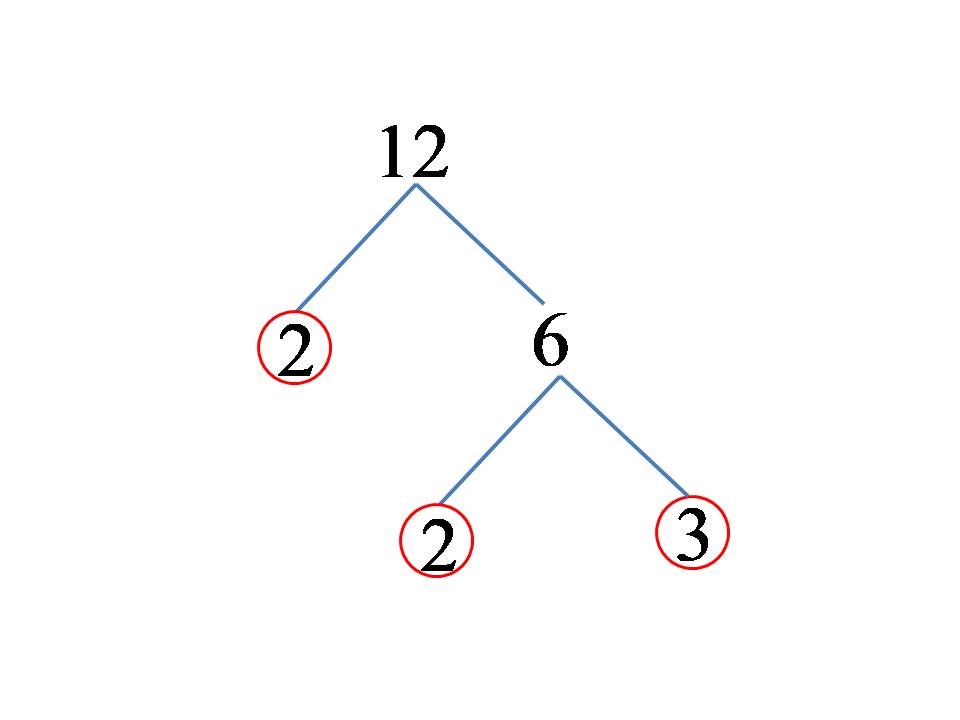
Број 12, након што се растављи на његове просте чиниоце, може се написати у следећем облику:
12 = 2 x 2 x 3
Табела Растављање На Просте Чиниоце За Бројеве Од 1 До 100
Табела која вам је доступна у наставку садржи све бројеве од 1 до 100. У њој можете видети податке о томе који су бројеви од 1 до 100 прости бројеви. Штавише, овде је табела представља поделу свих сложених бројева од 1 до 100 на њихове просте чиниоце.
| Број | Растављање (Ако је могуће) |
|---|---|
| 1 | Прост број |
| 2 | Прост број |
| 3 | Прост број |
| 4 | 4 = 2 x 2 |
| 5 | Прост број |
| 6 | 6 = 2 x 3 |
| 7 | Прост број |
| 8 | 8 = 2 x 2 x 2 |
| 9 | 9 = 3 x 3 |
| 10 | 10 = 2 x 5 |
| 11 | Прост број |
| 12 | 12 = 2 x 2 x 3 |
| 13 | Прост број |
| 14 | 14 = 2 x 7 |
| 15 | 15 = 3 x 5 |
| 16 | 16 = 2 x 2 x 2 x 2 |
| 17 | Прост број |
| 18 | 18 = 2 x 3 x 3 |
| 19 | Прост број |
| 20 | 20 = 2 x 2 x 5 |
| 21 | 21 = 3 x 7 |
| 22 | 22 = 2 x 11 |
| 23 | Прост број |
| 24 | 24 = 2 x 2 x 2 x 3 |
| 25 | 25 = 5 x 5 |
| 26 | 26 = 2 x 13 |
| 27 | 27 = 3 x 3 x 3 |
| 28 | 28 = 2 x 2 x 7 |
| 29 | Прост број |
| 30 | 30 = 2 x 3 x 5 |
| 31 | Прост број |
| 32 | 32 = 2 x 2 x 2 x 2 x 2 |
| 33 | 33 = 3 x 11 |
| 34 | 34 = 2 x 17 |
| 35 | 35 = 5 x 7 |
| 36 | 36 = 2 x 2 x 3 x 3 |
| 37 | Прост број |
| 38 | 38 = 2 x 19 |
| 39 | 39 = 3 x 13 |
| 40 | 40 = 2 x 2 x 2 x 5 |
| 41 | Прост број |
| 42 | 42 = 2 x 3 x 7 |
| 43 | Прост број |
| 44 | 44 = 2 x 2 x 11 |
| 45 | 45 = 3 x 3 x 5 |
| 46 | 46 = 2 x 23 |
| 47 | Прост број |
| 48 | 48 = 2 x 2 x 2 x 2 x 3 |
| 49 | 49 = 7 x 7 |
| 50 | 50 = 2 x 5 x 5 |
| 51 | 51 = 3 x 17 |
| 52 | 52 = 2 x 2 x 13 |
| 53 | Прост број |
| 54 | 54 = 2 x 3 x 3 x 3 |
| 55 | 55 = 5 x 11 |
| 56 | 56 = 2 x 2 x 2 x 7 |
| 57 | 57 = 3 x 19 |
| 58 | 58 = 2 x 29 |
| 59 | Прост број |
| 60 | 60 = 2 x 2 x 3 x 5 |
| 61 | Прост број |
| 62 | 62 = 2 x 31 |
| 63 | 63 = 3 x 3 x 7 |
| 64 | 64 = 2 x 2 x 2 x 2 x 2 x 2 |
| 65 | 65 = 5 x 13 |
| 66 | 66 = 2 x 3 x 11 |
| 67 | Прост број |
| 68 | 68 = 2 x 2 x 17 |
| 69 | 69 = 3 x 23 |
| 70 | 70 = 2 x 5 x 7 |
| 71 | Прост број |
| 72 | 72 = 2 x 2 x 2 x 3 x 3 |
| 73 | Прост број |
| 74 | 74 = 2 x 37 |
| 75 | 75 = 3 x 5 x 5 |
| 76 | 76 = 2 x 2 x 19 |
| 77 | 77 = 7 x 11 |
| 78 | 78 = 2 x 3 x 13 |
| 79 | Прост број |
| 80 | 80 = 2 x 2 x 2 x 2 x 5 |
| 81 | 81 = 3 x 3 x 3 x 3 |
| 82 | 82 = 2 x 41 |
| 83 | Прост број |
| 84 | 84 = 2 x 2 x 3 x 7 |
| 85 | 85 = 5 x 17 |
| 86 | 86 = 2 x 43 |
| 87 | 87 = 3 x 29 |
| 88 | 88 = 2 x 2 x 2 x 11 |
| 89 | Прост број |
| 90 | 90 = 2 x 3 x 3 x 5 |
| 91 | 91 = 7 x 13 |
| 92 | 92 = 2 x 2 x 23 |
| 93 | 93 = 3 x 31 |
| 94 | 94 = 2 x 47 |
| 95 | 95 = 5 x 19 |
| 96 | 96 = 2 x 2 x 2 x 2 x 2 x 3 |
| 97 | Прост број |
| 98 | 98 = 2 x 7 x 7 |
| 99 | 99 = 3 x 3 x 11 |
| 100 | 100 = 2 x 2 x 5 x 5 |
| 101 | Прост број |
Видео примери
Препоручљиво је погледати видео који садржи све растављање на просте чиниоце на сложених бројева од 1 до 100. У видеу имате прилику да видите како се растављање дешава корак по корак користећи методологију представљања кроз гране множитеља.
Tags: Множитеље, Просте, Растављање, Чиниоце

 Сачекајте...
Сачекајте...