Проширивање и скраћивање разломака? Хајде да научимо како да проширимо и скратимо разломке! Овај математички поступак и вештина су веома важни ако желите да савладате све теже кораке са којима ћете се суочити у будућности када учите математику!
Важно је напоменути да кад год се проширивање и скраћивање разломака заврши на исправан начин, добија се еквивалентни разломак који има исту нумеричку вредност као и оригинални разломак који смо почели да ширимо или скраћујемо. Најчешће се при сабирању разломака користи поступак проширења разломака ако се њихови имениоци међусобно разликују. Затим морамо проширити разломке на исти именилац пре него што израчунамо њихов збир.
Проширивање И Скраћивање До Еквивалентни Разломак
То је једноставно! Да би се из разломка добио његов еквивалентни разломак, то се може учинити на само два начина. Су:
- Проширивањем разломка
- Скраћивањем разломка
Скраћивање Разломака
Први начин да одредите еквивалентни разломак који ћемо приказати на овој страници је скраћивање разломка. Скратити разломак значи поделити његов бројилац и именилац истим целим бројем који је њихов заједнички делилац.
Истовремено, бројилац и именилац се могу поделити било којим својим заједничким делиоцем, не водећи рачуна да им је то увек највећи заједнички делилац. Једина разлика је у томе што ако поделимо са њиховим највећим заједничким делиоцем, онда ћемо разломак одмах свести на његов најједноставнији облик. С друге стране, ако поделимо са неким од њихових других заједничких делилаца, резултујући разломак ће поново бити скраћен!
Погледајмо пример у којем ћемо извршити скраћивање разломака. Такав је случај са бројем 1 испод!
Пример Скраћивања Разломка
Пример 1: Скратите разломак дат на слици испод!
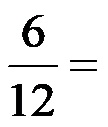
Разломак који покушавамо да скратимо има бројилац 6 и именилац 12. Очигледно, разломак можемо скратити дељењем са више бројева јер бројеви 6 и 12 имају више заједничких делилаца. Стога ћемо скраћивање извршити на два начина.
Први начин: Хајде да прво скратимо разломак бројем 3! То значи да морамо и његов бројилац и именилац поделити бројем 3. Скраћивање би требало да изгледа овако:
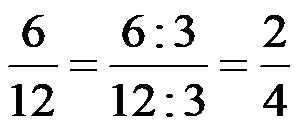
Други начин: Ако одлучимо да разломак скратимо на његов најједноставнији облик (стање у којем се више не може скратити), онда морамо да скратимо разломак бројем 6, јер је број 6 највећи заједнички делилац бројева 6 и 12. Скраћивање истог разломка из примера број 1 са бројем 6 треба да изгледа овако:
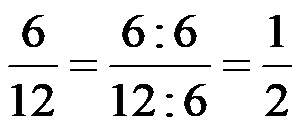
Очигледно, добијени разломак помоћу друге методе је у свом најједноставнијем облику и не може се даље скратити!
Проширивање Разломака
Поступак за проширење разломка је обрнут од поступка за скраћивање разломка. Ако се при скраћивању користи дељење математичке операције, приликом проширења треба користити множење математичке операције! Ако желимо да проширимо разломак, онда треба да у исто време помножимо његов бројилац и именилац истим целим бројем.
Истовремено, важно је од почетка знати да уопште не постоји ограничење на то како би цео број требало да буде. Можемо једноставно користити било који цео број да проширимо разломак!
Пример Проширења Разломка
Пример 2: Проширите разломак на слици испод!
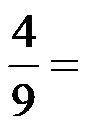
Разломак из примера 2 има бројилац 4 и именилац 9. Проширимо разломак бројем 3! То значи да морамо истовремено помножити и бројилац и именилац бројем 3. Проширење разломка би требало да изгледа овако:
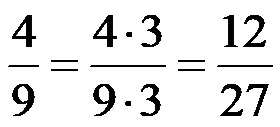
Ако желимо да проширимо исти почетни разломак из примера 2 бројем 10, то значи да треба да помножимо и бројилац и његов именилац бројем 10. Проширивање разломка за 10 треба да изгледа овако:
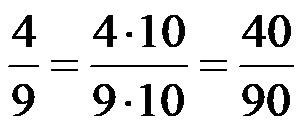
Видео испод вам омогућава да видите многе примере за проширивање и скраћивање разломака! Искористите прилику да се тестирате да видите да ли разумете поенту проширења и скраћивања разломака!
Радни Листови
Кликом на дугме за преузимање испод, сваки од наших читалаца може добити Microsoft Word документ који садржи математичке задатке за проширење и скраћивање разломака. Препоручујемо вам да користите ове материјале да бисте успешно завршили процес учења проширења и скраћивања разломака!
Tags: Пример, Прошривање, Разломака, Скраћивање

 Сачекајте...
Сачекајте...