Знате ли шта показује Питагорина теорема? Да ли знате да је једна од најпознатијих, најважнијих и најкоришћенијих теорема у геометрији Питагорина теорема? Овде на овој страници испод можете прочитати доста информација о овој чувеној математичкој теореми, њеној дефиницији, значењу и конкретној примени у решавању математичких задатака из области геометрије.
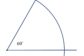
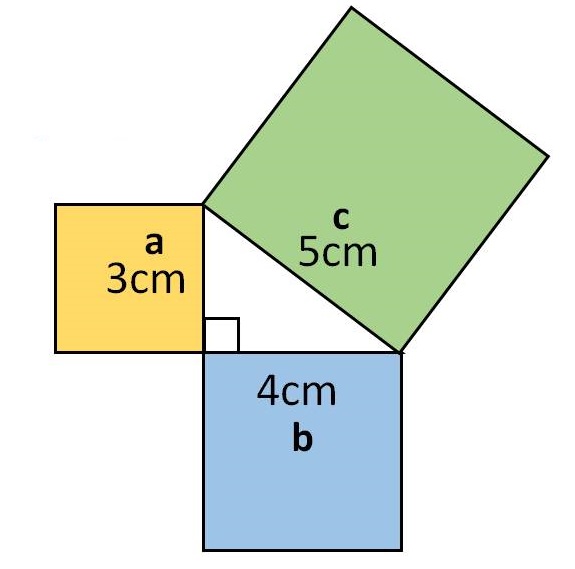
Сама дефиниција Питагорине теореме гласи: У правоуглом троуглу, квадрат који се може формирати над хипотенузом (квадрат са страницом исте дужине као хипотенуза) има исту површину као збир површина квадрата који се на исти начин може формирати преко својих кракова (две краће странице правоуглог троугла). Ово правило правоуглог троугла је открио Питагора!
Да се укратко подсетимо како се зову различите странице правоуглог троугла. Страна са најдужом дужином увек је означена словом c (мало латинично слово c) и назива се хипотенуза. Две странице правоуглог троугла које су краће од хипотенузе називају се катетама и означавају се са a и b (мала латинична слова a и b). У правоуглом троуглу, угао између катета (странице a и b) је увек раван, односно износи тачно 90 степени. Друга два угла (углови који се налазе на хипотенузи су увек оштри, тј. њихова величина је мања од 90 степени. Кликните овде да видите које врсте углова постоје!
Питагорина Теорема И Њена Формула
Једна од најчешће коришћених формула у геометрији и математици, формула која описује Питагорину теорему је:
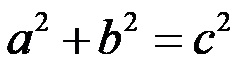
Састав формуле за Питагорину теорему омогућава нам да је користимо за израчунавање дужине једне непознате странице правоуглог троугла, ако су друге две стране познате. На пример, ако су познате дужине катета, онда се дужина хипотенузе може лако израчунати, или ако је позната дужина хипотенузе и једног од катета, онда се може лако одредити дужина другог крака.
У наставку у неколико примера можете видети како се Питагорина теорема примењује за одређивање дужине непознате странице у правоуглом троуглу! Препоручујемо вам да погледате примере у наставку!
Примери
Пример 1. Израчунај дужину хипотенузе правоуглог троугла, ако је познато да су дужине његових катета 8cm и 15cm!
У овој ситуацији, када је позната дужина два крака, можемо одмах да заменимо њихову дужину у формули за Питагорину теорему. Ова замена вредности даје израз дат на слици испод!
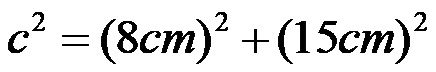
У следећем кораку степенујемо обе вредности, тако да добијамо:
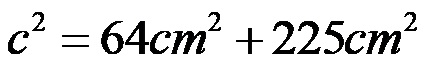
Израчунавамо збир новодобијених вредности:
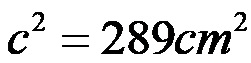
Коначно, да бисмо израчунали дужину хипотенузе, израчунавамо корен бројчане вредности која се налази на десној страни једначине.
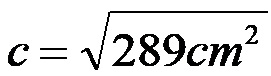
Дужина хипотенузе правоуглог троугла из примера 1 је 17 центиметара!
Логично, могућности које нуди Питагорина теорема важе и за израчунавање дужине непознатог крака ако су познати други крак и хипотенуза. У тој ситуацији, о томе како је непозната нога означена у конкретном случају, може се користити једна од следећих формула при решавању:

Ако је крак са ознаком a непознат, користите формулу са леве стране, али ако је ног са ознаком b непознат, користите формулу са десне стране!
Хајде да решимо такав пример! Погледајте пример 2 у наставку!
Пример 2. Правоугли троугао има хипотенузу дужине 29 дециметара. Израчунај дужину једног његовог крака, ако је други крак дужине 21 дециметар!
Ако дужину непознатог крака означимо са a, онда можемо директно користити трансформисану формулу на левој страни изнад, обојену црвеном бојом. Заменом датих вредности за хипотенузу и познати крак, добија се израз:
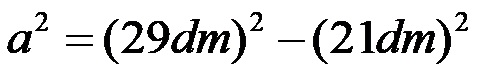
Ми степенујемо:
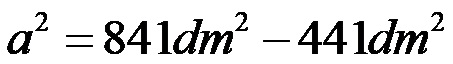
Израчунавамо разлику бројева:
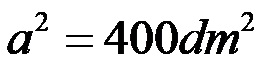
Коначно коренимо!
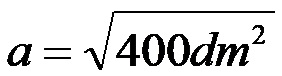
Дужина непознатог крака из другог примера је 20 дециметара!
Примена Питагорина Теореме
Препоручујемо да погледате садржај видеа испод! У њему можете видети како је теорема дефинисана, неколико примера израчунавања дужине непознате странице као и неколико комбинација Питагориних тројки (цели бројеви који могу бити дужине страница правоуглог троугла).
Питагорина теорема се широко користи у геометрији и математици уопште. Присуство правоуглог троугла у правилним геометријским телима, простору, имагинарним облицима, телима и простору, омогућава да се ова теорема користи у многим различитим ситуацијама и помаже у решавању многих математичких проблема. Многи од успеха постигнутих у области тригонометрије остварени су захваљујући овој теореми.
Tags: Дефиниција, Задатак, Катета, Питагорина, Правоугли, Пример, Теорема, Троугао, Хипотенуза

 Сачекајте...
Сачекајте...