Осна симетрија је врста геометријске трансформације у којој се симетрија одређује или покреће на две различите стране у односу на главну оптичку осу (линију).
Оса Симетрије
Штавише, ако се две тачке (под углом од 90 степени) налазе на две различите стране осе симетрије, на истој удаљености и у истој равни, онда се те две тачке сматрају симетричним у односу на ту осу од симетрије!
Слично, ако су све тачке геометријске фигуре подједнако удаљене на две различите стране у истој равни као и друга геометријска фигура, онда се за те две геометријске фигуре може рећи да су симетричне у односу на ту ос симетрије.
Оса симетрије се може одредити чак и за једну фигуру, ако се та геометријска фигура може поделити на два идентична дела која задовољавају горе наведене услове симетрије у односу на дату осу симетрије! Ученици најчешће размишљају о томе да ли се геометријска фигура може савити на пола, па ако је могуће место савијања је управо сама оса симетрије!
Осносиметричне Фигуре
Неке од најпознатијих геометријских фигура припадају класи ососиметричних фигура! Геометријска фигура је осносиметрична ако има бар једну осу симетрије! Наравно, постоје и такве геометријске фигуре које имају више од једне осе симетрије!
Погледајмо неке карактеристичне геометријске фигуре које су осносиметричне!
Осносиметричне геометријске фигуре укључују:
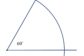
Једнакостранични троугао има три осе симетрије!
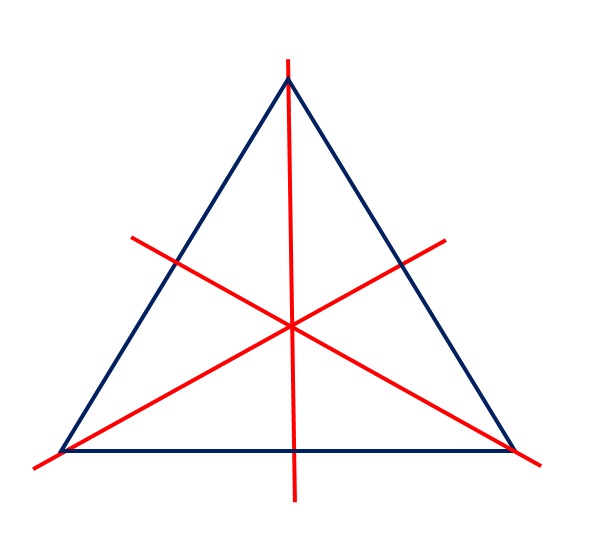
Једнакокраки троугао има једну осу симетрије!
Да ли знате како израчунати површину једнакокраког троугла?
Правоугаоник има две осе симетрије!

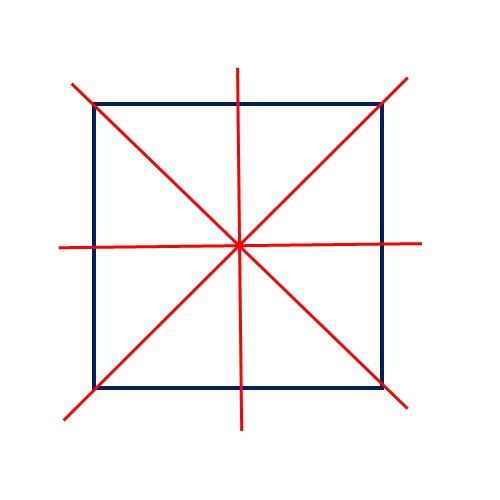
Квадрат има четири осе симетрије!
Једнакокраки трапез има једну осу симетрије!
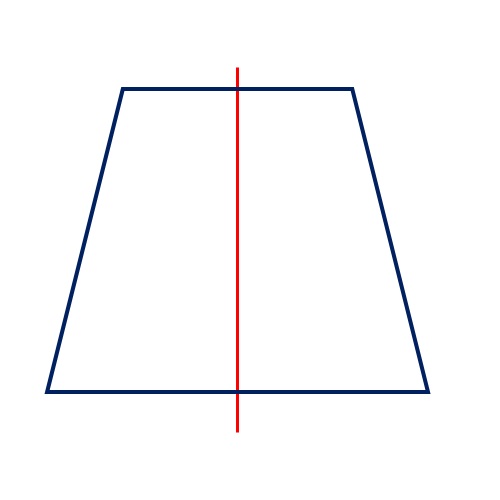
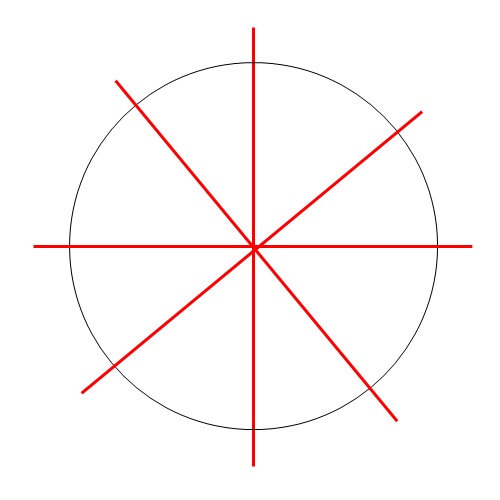
Круг има бесконачно много оса симетрије!
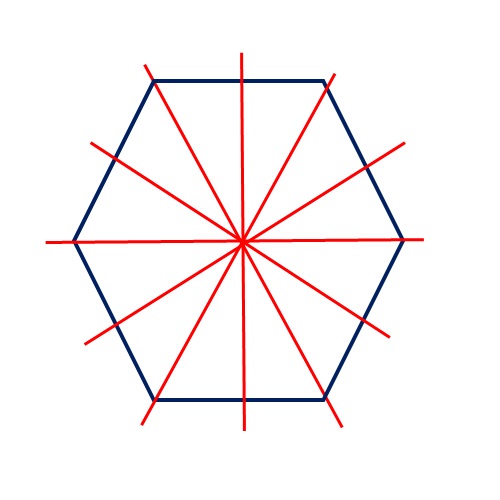
Неке геометријске фигуре које имају више од четири стране или углове могу имати осу симетрије, али најчешће су то такозвани правилни многоуглови, чије су странице и углови међусобно једнаки! Пример правилан шестоугао има шест оса симетрије!
Погледајте како да конструишете симетралу угла!
Осна Симетрија У Координатном Систему
Као тип геометријске трансформације, често морамо да користимо осну симетрију у координатном систему са стриктно дефинисаном осом симетрије датом у односу на к,и координатну осу или било коју другу линију која је опет дала одређене вредности у односу на x оси или y оси.
Сама чињеница да би две геометријске фигуре биле симетричне у односу на осу симетрије, њихове одговарајуће тачке треба да буду подједнако удаљене од осе, говори о томе да када је симетричну фигуру потребно одредити геометријски, довољно је добити сваку његових тачака на једнакој удаљености од осе на супротној од њега!
Пажљиво погледајте слике испод да бисте разумели шта тачно треба да се уради!
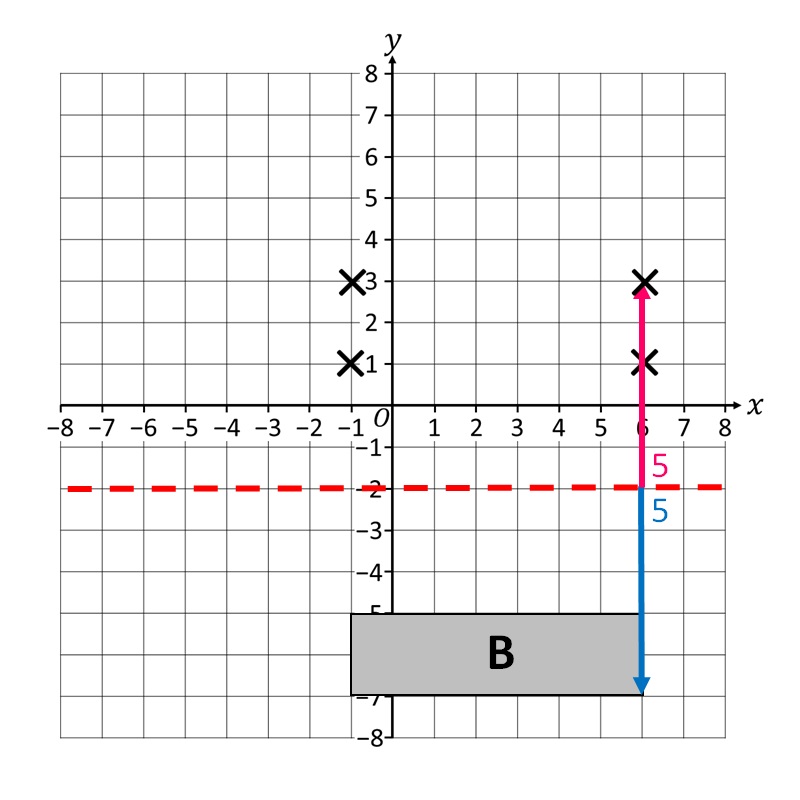
Пример 1. Конструисати слику геометријске фигуре B са осном симетријом у односу на осу симетрије y= -2!
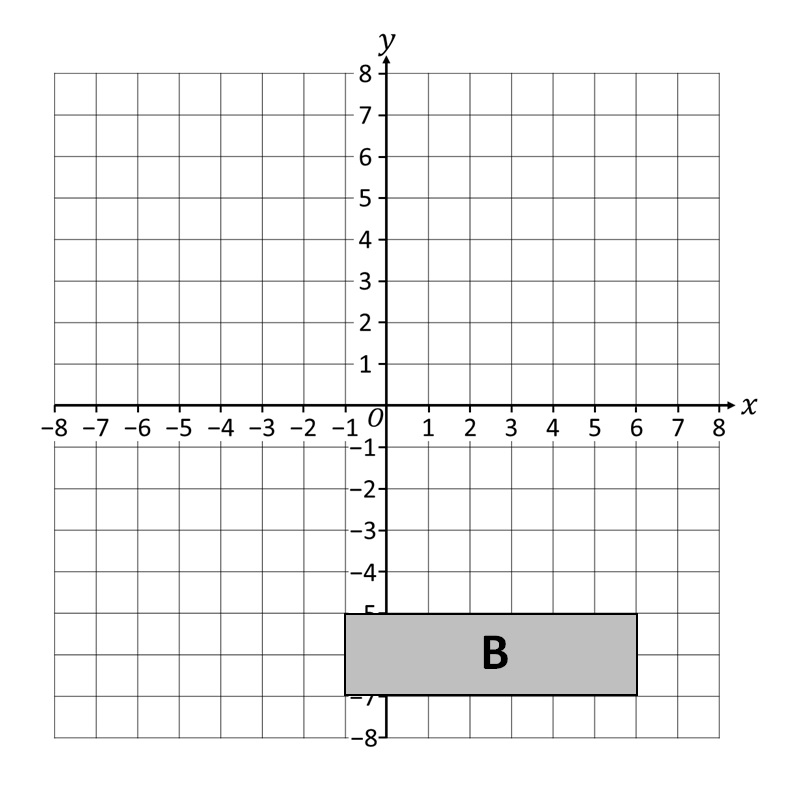
Прво нацртамо осу симетрије y=-2!
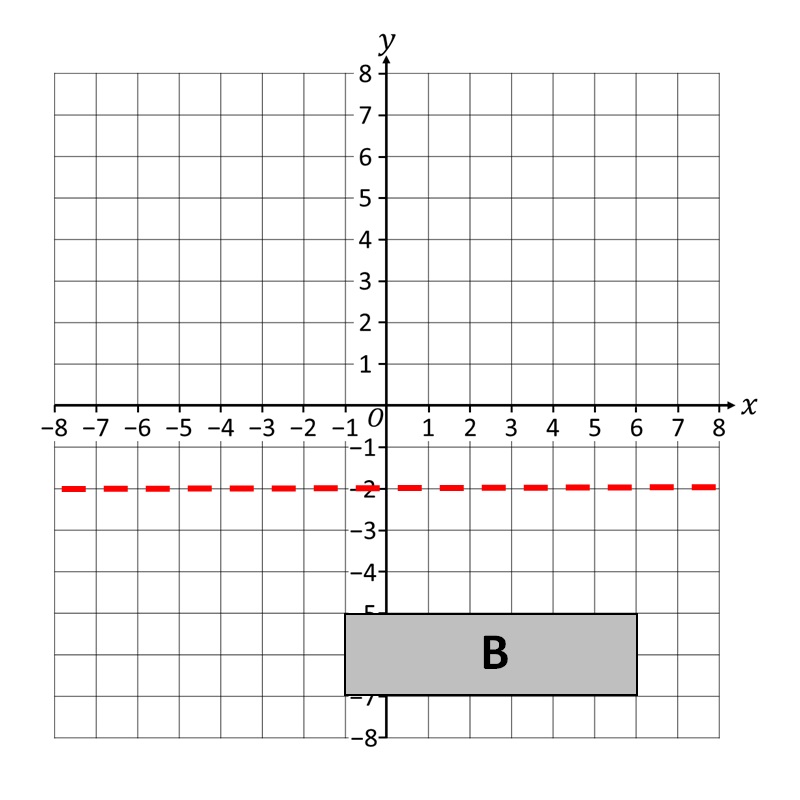
Затим за сваки врх геометријске фигуре B одредимо његову одговарајућу слику на једнакој удаљености од супротне стране осе симетрије. Почећемо са првим!
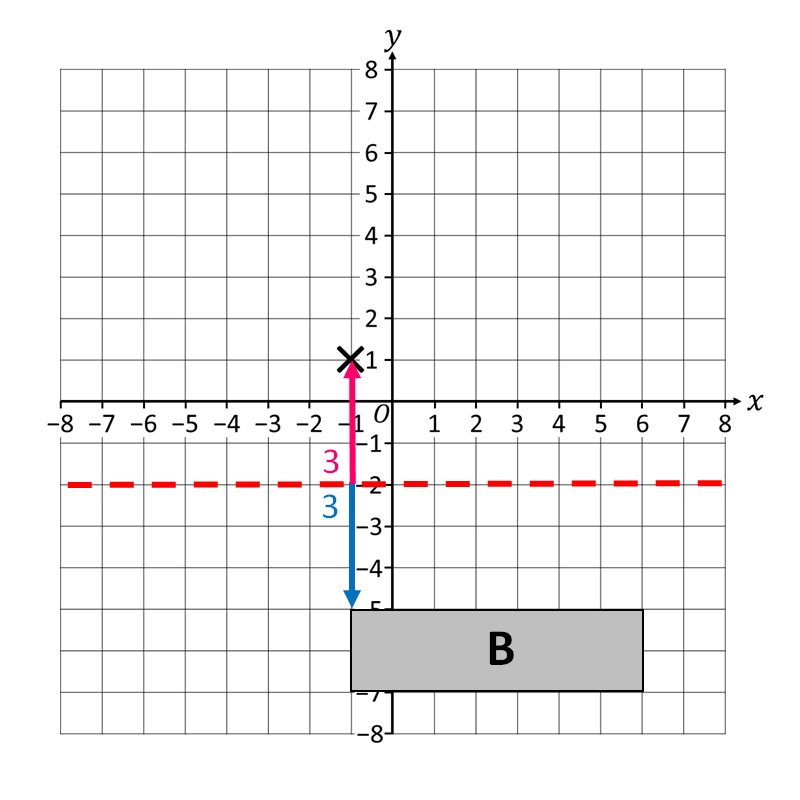
Други долази!
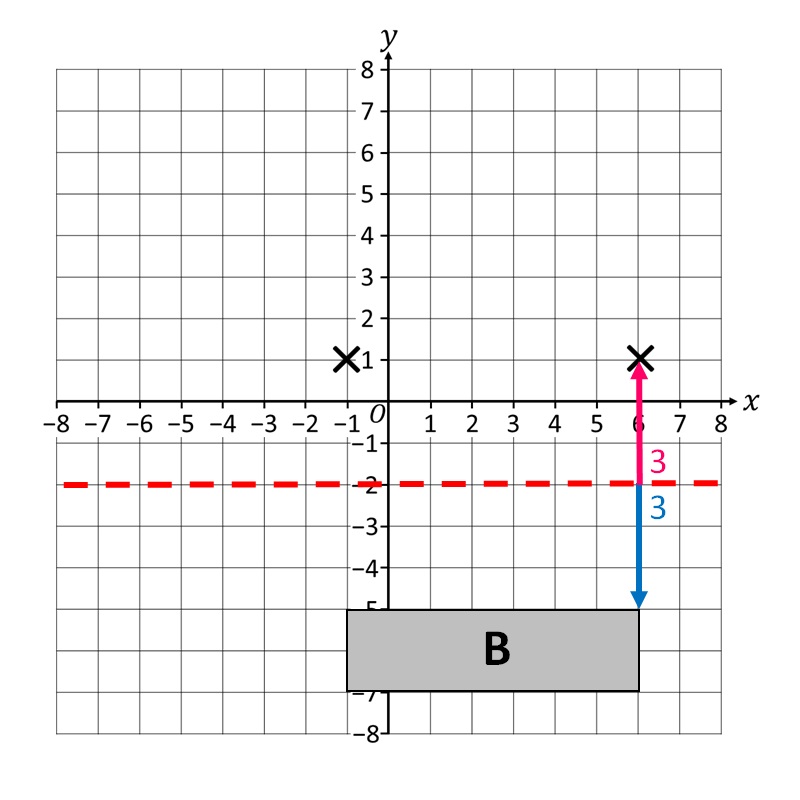
Затим мапирамо и трећи!
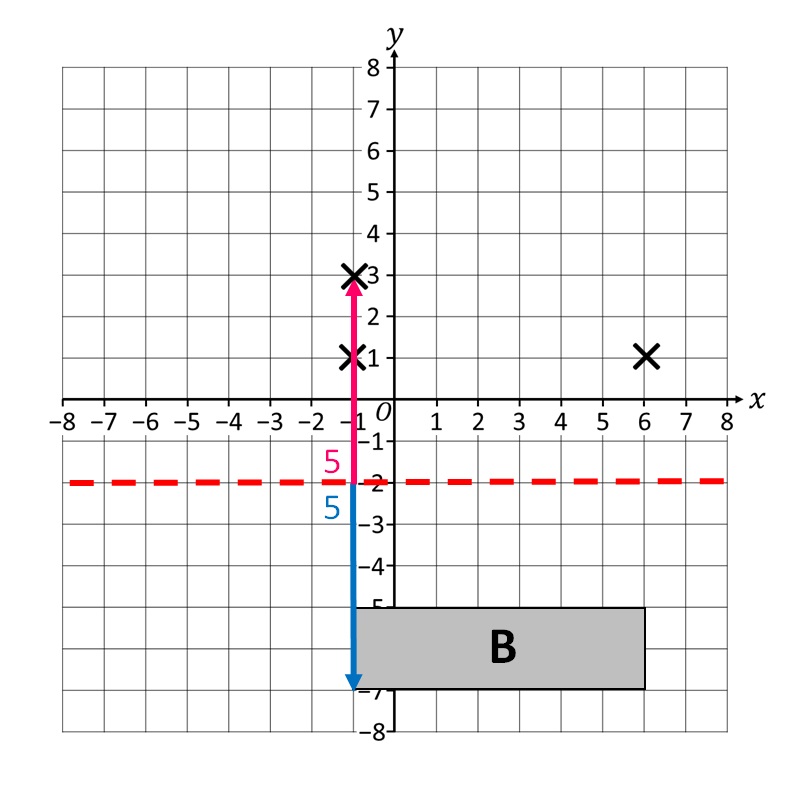
Коначно, завршавамо са пресликавањем последњег темена!
Последњи корак је да нацртате целу слику, која одговара и симетрична са геометријском фигуром B! Коначни резултат би требао изгледати као на слици испод!
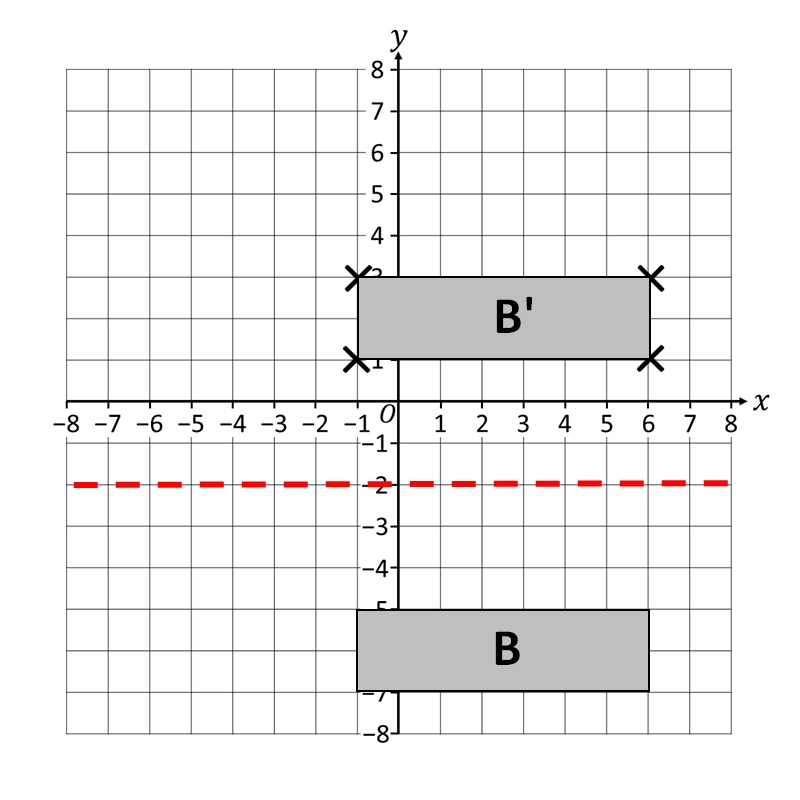
Уопште није тешко, зар не? Само треба да се потрудите да будете прецизни како би слика била што јаснија и прецизнија, а самим тим и лепша!
Видео Примери
Видео материјал, коме можете приступити кликом на доњу икону видеа, даје вам приступ изузетно јасно представљеним примерима осиметричног пресликавања у координатном систему. Препоручујемо вам да погледате ове примере како бисте разумели разлику у односу на различито постављене и дефинисане осе симетрије!

 Сачекајте...
Сачекајте...