Које вештине треба да имате да бисте успешно израчунали обим и површина сложених фигура? Овде у овом тексту ћемо описати све што треба да знате да бисте могли да израчунате обим и површину сложених геометријских 2Д фигура. Истовремено ћемо ићи корак по корак у објашњењима како би сваки читалац могао да разуме поенту решавања ових математичких задатака.
Потребна Знања И Вештине За Обим И Површина Сложених Фигура
Свако ко покушава да реши проблем израчунавања обим и површине сложених фигура треба да зна појединачне формуле за израчунавање обим и површине карактеристичних 2Д фигура као што су квадрат, правоугаоник, ромб итд.
Понекад је у појединачним задацима веома важно логичким размишљањем извући тачне закључке о дужини неких страница сложене геометријске фигуре која се на почетку уопште не зна. Међутим, у тим ситуацијама има довољно почетних података о тој страни, или о том делу те стране, да се може без проблема утврдити. Наша препорука је да будете опрезни у тим конкретним ситуацијама јер је врло лако погрешити!
Хајде да размотримо једну такву ситуацију у којој треба да одредимо дужину странице сложене геометријске фигуре која није позната! Погледајте пример у наставку!
Пример 1. Колика је дужина непознате странице сложене геометријске фигуре дате на доњој слици?
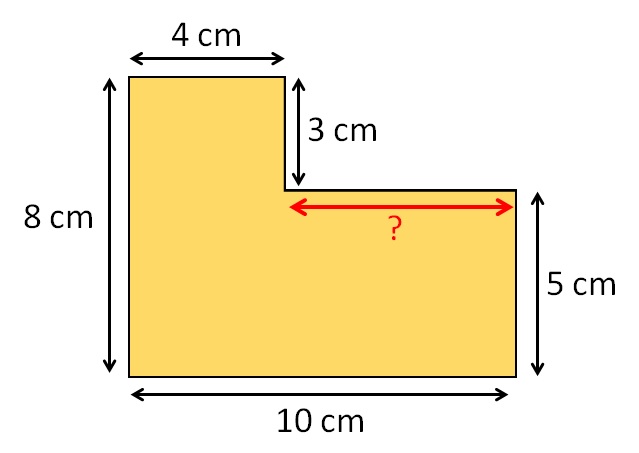
Непозната страна је означена црвеном бојом! Очигледно, дужина те непознате странице може се одредити као разлика између паралелних страница према непознатој страни. Логично, одузимамо краћу страну од дуже стране, или:
10cm – 4cm = 6cm
Дужина непознате странице је 6 центиметара!
Обим Сложене Геометријске Фигуре
Ако имате сва потребна знања и вештине које су горе наведене, онда можете приступити одређивању обима сложене геометријске фигуре. Да би се одредио обим, треба израчунати збир свих страна сложене фигуре. У другом примеру ћемо вам помоћи да израчунате обим сложене фигуре за коју смо већ одредили дужину непознате странице у примеру број један. Да видимо како то изгледа!
Пример 2. Израчунајте обим сложене фигуре дате на слици испод!
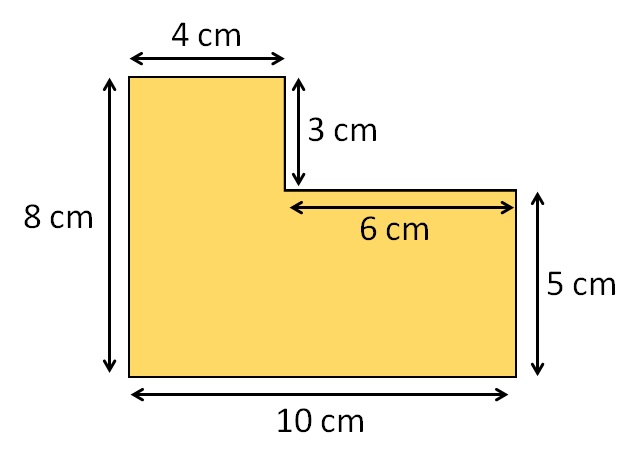
Једноставно изаберемо почетну тачку одакле желимо да почнемо и израчунамо збир дужина свих страна сложене геометријске фигуре. При томе пазите да не изоставите ниједну страну јер ће нас то довести до погрешног решења!
Обрачун би требало да изгледа овако:
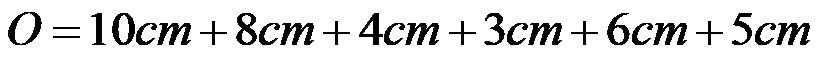
Обим сложене фигуре је 36 центиметара!
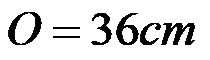
Површина Сложене Фигуре
Поступак за израчунавање површине сложене фигуре је компликованији математички поступак од израчунавања њеног обима. Да бисмо израчунали површину, морамо замислити сложену фигуру као комбинацију правилних геометријских 2Д облика. Ако целу његову површину представимо као комбинацију површина квадрата, правоугаоника или неког другог правилног 2Д облика, онда је збир њихових површина заправо површина сложеног геометријског облика.
Понекад можемо чак и да замислимо спољашње делове сложене фигуре који заједно са њом граде неки правилан геометријски облик. У том случају задатак се може израчунати као разлика између целине (сложена фигура + спољашњи део) и спољашњег дела.
Као што се лако разуме, површина сложене фигуре може се израчунати на неколико начина. У наставку ћемо представити како израчунати површину исте сложене фигуре на два различита начина!
Површина Сложене Фигуре Као Збир Унутрашњих Фигура
Вратимо се нашој сложеној фигури чију смо непознату страну и обим већ одредили! Размотрите пажљиво решење следећег примера!
Пример 3. Израчунајте површину сложене фигуре чији смо обим већ одредили у претходном примеру!
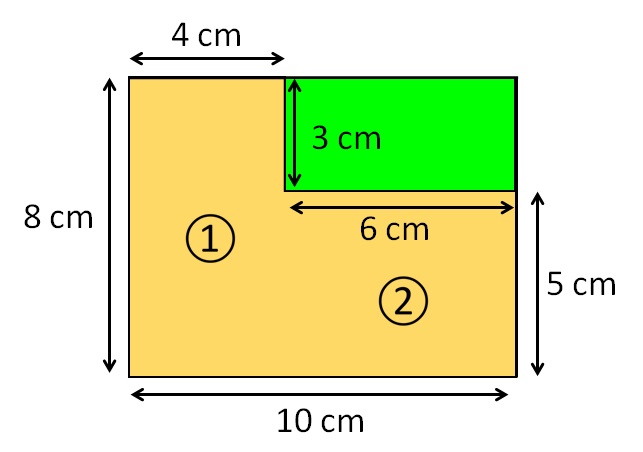
Наш први циљ у овој ситуацији је да ову сложену фигуру представимо као комбинацију неколико правилних фигура! Једна таква прилика је представљена на слици испод!
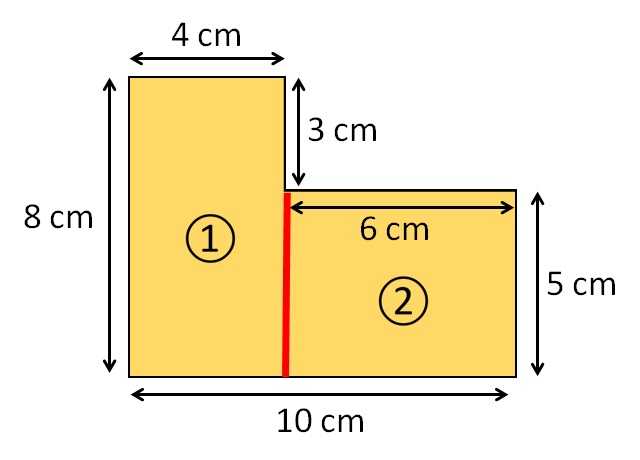
Бројеви 1 и 2 означавају два различита правоугаоника који заједно покривају целу површину сложене фигуре. Дакле, површина два правоугаоника заједно има исту површину као и сложена фигура. Овде са P индексом 1 означавамо површину први дио, а са P индексом 2 површину зелени део. Дакле, можемо израчунати површину сложене фигуре користећи формулу за површину правоугаоника, на следећи начин:
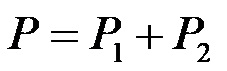
Уносимо формулу за одређивање површина правоугаоника!
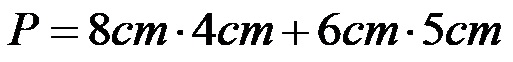
Израчунавамо појединачне производе.
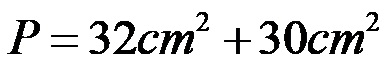
На крају сабирамо две вредности!
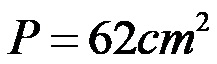
Површина сложене фигуре са првом методом је 62 квадратна центиметра!
Површина Сложене Фигуре Са Имагинарних Делова
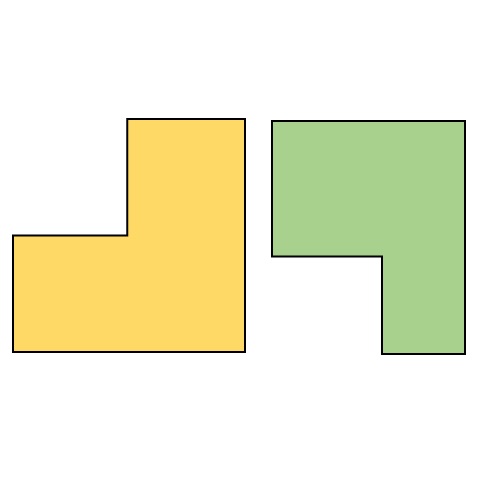
Исту геометријску сложену фигуру из трећег примера представићемо као замишљену целу правилну геометријску фигуру! Једна таква могућност је дата на слици испод:
Са горње слике је јасно да сложеној фигури прво додамо један додатни део (део који је обојен зелено) са којим та фигура заједно гради правоугаоник. Врло је лако видети да ако посматрамо ствари на овај начин, онда се површина сложене фигуре може израчунати као разлика између површине целе фигуре (сложена фигура + зелено) и додатне површине ( зелени део). Овде са P индексом c означавамо површину целе фигуре, а са P индексом z зелени део. Израчун је дат у наставку!
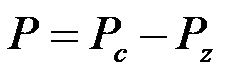
Прво уносимо формулу за површину правоугаоника (оба облика су правоугаона).
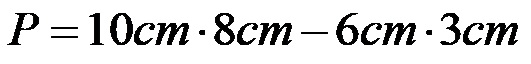
Сада израчунавамо појединачне производе!
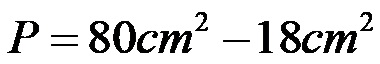
Коначно, одузимамо две вредности!
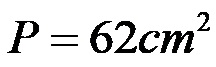
Површина сложене фигуре са другом методом је 62 квадратна центиметра!
Још један доказ да се исти математички проблем може решити на много различитих начина. Овај пример потврђује да при одређивању површине сложене фигуре, како год мислимо, све док то радимо на прави начин можемо доћи до тачног решења.
Видео примери
Видео материјал у наставку садржи много занимљивих примера израчунавања обим и површина сложених фигура. Погледајте што више примера да бисте размотрили различите проблемске ситуације које ће вам помоћи да у будућности лако решите проблеме у којима треба да израчунате обим и површина сложених фигура!
Tags: Геометријски, Обим, Површина, Сложених, Фигура, Формула

 Сачекајте...
Сачекајте...