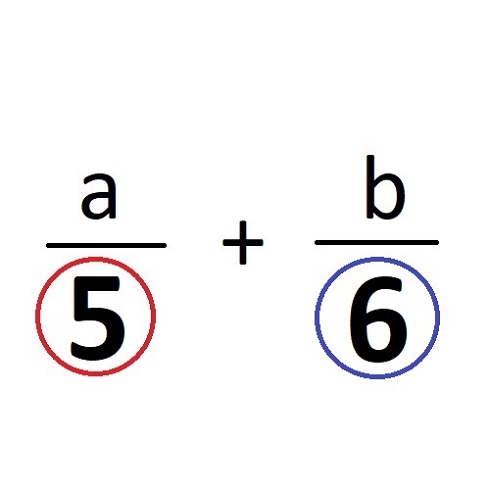
Овај одељак наше веб странице треба да послужи свим нашим читаоцима да науче како да пронађу најмањи заједнички садржалац (НЗС) два или више бројева. Поступак је изузетно важан јер се примењује као додатни поступак при решавању многих математичких задатака. Место где се дефинитивно најчешће користи је при сабирању разломака који немају исте имениоце. Затим, први део тог задатка се увек своди на одређивање најмањег заједничког имениоца (НЗС), који је опет синоним за најмањи заједнички садржалац, односно ради се о истој ствари. Почетна слова три речи стварају скраћеницу која се користи у овом случају НЗС!
У наставку на овој страници можете видети још примера у којима описујемо шта треба урадити да би се успешно одредио најмањи заједнички садржалац два или више бројева.
Прво ћемо почети решавањем најлакшег задатка који укључује само два броја. Хајде да прво урадимо то:
Најмањи Заједнички Садржалац Разлагањем Простих Бројева
Дефиниција: Најмањи заједнички садржалац два или више бројева је њихов најмањи заједнички садржалац. То је најмањи могући број који, када се подели сваким од бројева, даје количник који је цео број без добијања остатка.
Први пример испод садржи упутства о томе како израчунати НЗС за два броја со разлагањем простих бројева! Погледајте објашњење и решење!
Пример 1: Одредити најмањи заједнички садржалац бројева 8 и 12!
Да бисмо одредили најмањи заједнички садржалац бројева 8 и 12, морамо прво та два броја раставити у њихове просте бројева. Декомпозиција даје следеће изразе:
8 = 2 x 2 x 2
12 = 2 x 2 x 3
Множењем простих бројева на два броја добија се производ. Тај производ је најмањи заједнички садржалац два броја. Бити пажљив! Приликом израчунавања производа једноставне умножаке који су у оба броја записујемо само једном! Обрачун би требало да изгледа овако:
НЗС (8;12) = 2 x 2 x 2 x 3 = 24
Ако желимо да проверимо истинитост решења, онда ћемо заиста утврдити да је број 24 најмањи број који, када се подели бројевима 8 и 12, нема остатка! Коначно, утврђујемо да је број 24 НЗС 8 и 12!
Процедура је иста ако треба да израчунате НЗС за више од два броја! С друге стране, иако је поступак идентичан, потребно је више времена за решавање јер има више бројева које треба урачунати у њихове основне факторе. Израчунавање НЗС на три броја садржи други пример у наставку! Погледајте и следећи пример:
Пример са три броја
Пример 2: Одреди НЗС за бројеве 5, 15 и 25!
Поново практикујемо исти поступак! Прво треба да урачунамо сва три броја у њихове просте бројева. Тај распад би требао изгледати овако:
5 = 1 x 5
15 = 3 x 5
25 = 5 x 5
Водећи рачуна да сви разложени бројеви садрже најмање по један 5, остаје да помножимо све просте бројева један са другим и израчунамо најмањи заједнички садржалац бројева 5, 15 и 25. Коначно решење је дато у наставку:
НЗС (5;15;25) = 3 x 5 x 5 = 75
Увек је лепо да сами проверимо решење које смо добили у решеним задацима из математике. Зато, хајде да проверимо да ли ће резултат добијен дељењем појединачним бројевима омогућити да добијемо количник који је цео број, односно количник без остатка. Погледајте чек који је дат у наставку!
75:5 = 15
75:15 = 5
75:25 = 3
Закључујемо да је број 75 заиста најмањи заједнички садржалац бројева 5, 15 и 25!
Целокупна процедура коришћена у два решена примера изнад може се генерализовати и користити без икаквих проблема у свим оним ситуацијама када је потребно одредити НЗС од три, четири, пет или више бројева.
Корисна Методологија
Наравно, постоји алтернативни метод за одређивање НЗС од два или више бројева, који је заправо лакши и краћи. У видеу у прилогу испод можете видети како се најмањи заједнички садржалац може израчунати скраћеном методом коју ученици често користе приликом решавања математичких задатака у школи. Овде, као иу многим другим ситуацијама у математици, можете добити тачно решење користећи различите методе рада. Наравно, подразумева се да било коју од процедура треба да користите исправно!
Други Метод За Израчунавање Најмањи Заједничког Садржалац
У наставку у трећем и четвртом примеру можете видети како да израчунате најмањи заједнички садржалац два или више бројева формирањем низа садржалаца за сваки од бројева појединачно. Штавише, након што се низови формирају, потребно је видети који је најмањи број садржан у сваком низу. На овај начин се може тачно лоцирати НЗС тих бројева.
За почетак, у трећем примеру, да видимо како се практикује овај други метод за израчунавање НЗС:
Пример 3: Одредити најмањи заједнички садржалац бројева 6 и 8!
Прва фаза решења се своди на формирање низова контејнера за бројеве 6 и 8. Низови би требало да изгледају овако:
6: 6, 12, 18, 24, 30, …
8: 8, 16, 24, 32, 40, …
Након што су два појединачна низа већ формирана, још увек морамо да видимо да ли постоји исти број који је присутан у оба низа. Штавише, тај број би требало да буде најмањи од свих таквих бројева (ако их има више). У нашем случају је јасно да је то број 24. Можемо рећи да је 24 најмања заједничка компонента бројева 6 и 8:
Пример 4: Пронађите НЗС за бројеве 2, 4 и 5!
Настављамо на исти начин. Прво формирамо низове контејнера за сваки од бројева појединачно. Ти низови би требали изгледати овако:
2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, …
4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, …
5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 60, 55, …
Коначни низ нам јасно показује да је најмањи заједнички садржалац бројева 2, 4 и 5 број 20. Можемо записати да:
НЗС (2;4;5) = 20
Радни Лист
Ако већ добро разумете како да добијете најмањи заједнички садржалац два или више бројева, препоручујемо вам да преузмете радни лист доступан за преузимање испод. Овај радни лист садржи много примера у којима можете одредити најмањи заједнички садржалац (односно најмањи заједнички именилац) бројева који су имениоци разломака, тако да можете практично повезати овај поступак са тежим математичким операцијама које ћете треба да учим у будућности.
Видео Примери За Најмањи Заједнички Садржалац
Видео испод садржи решавање проблема помоћу друге методологије за израчунавање најмањег заједничког садржалац. Погледајте све те видео примере!
Поздрављамо информације о свим вашим додатним захтевима које имате, а који се на овај или онај начин односе на наш рад на овој веб страници! Хвала вам!
Tags: Заједнички, Именилац, Најмањи, Пример, Садржалац

 Сачекајте...
Сачекајте...