Множење децималних бројева је тежа математичка операција од множења природних бројева. Овде, осим поступка множења два децимална броја, морате пазити шта треба урадити са бројем децималних места које ће имати производ добијен на крају поступка. У наставку на овом месту можете видети како се множе децимални бројеви, али и како можете врло занимљивом техником лако израчунати производ два децимална броја без употребе калкулатора. Дозволите нам да вам представимо операцију множења децималних бројева на потпуно нов занимљив начин за који вероватно нисте чули раније. Препоручујемо вам да наставите са читањем текста у наставку!
Како Помножити Децималне Бројеве
Класичан начин множења децималних бројева укључује следеће кораке:
- Прво множимо бројеве као да немају децимални зарез (као да нису децимални бројеви).
- Након што добијемо производ, бројимо децимале у оба децимална броја и израчунавамо њихов збир. Пример ако први број има две децимале, а други три децимале, збир децималних места одређујемо као 2+3=5!
- Коначно, одредимо положај децималног зареза у производу тако што збир децималних места децималних бројева пренесемо у производ рачунајући с десна на лево. Ако два децимала имају укупно пет децимала, онда ће производ такође имати пет децимала!
Као што вероватно можете закључити из горњих корака, поступак множења децималних бројева је веома лак и подсећа на множење природних бројева с том разликом што треба обратити пажњу не на децимални зарез у самом производу!
Примери Множења Децималних Бројева
Хајде да употребимо горња правила да размотримо пример у коме ћемо помножити два децимална броја.
Пример 1. Израчунај производ децималних бројева датих на слици испод!
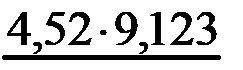
У примеру треба израчунати производ децималних бројева 4,52 и 9,123!
Решење је дато на слици испод!

Хајде да извршимо потпуну анализу датог резултата!
- Прво, помножимо све цифре првог децималног броја (децимални број са леве стране) са цифром 3 другог децималног броја. Јасно је да је 2 пута 3 6, 5 пута 3 је 15 (пишемо 5 и памтимо 1), 4 пута 3 је 12, а једно које памтимо је 13. Одавде следи да је 452 пута 3 1356.
- Затим помножимо све цифре првог децималног броја са цифром 2 другог децималног броја. Следи да је 2 пута 2 4, 5 пута 2 је 10 (пишемо 0 и памтимо 1), 4 пута 2 је 8 и једно које памтимо је 9. Одавде следи да је 452 пута 2 904.
- Следе множење цифром 1! 2 пута 1 је 2, 5 пута 1 је 5, а 4 пута 1 је 4. Јасно, 452 пута 1 је 452!
- Коначно, множимо са цифром 9 из другог децималног броја. 2 пута 9 је 18 (пишемо 8 и памтимо једно), 5 пута 9 је 45 и једно памтимо 46 (пишемо 6 и памтимо 4), 4 пута 9 је 36 и 4 памтимо 40. Из тога следи да је 452 пута 9 је 4068.
Приликом записивања појединачних производа треба водити рачуна да се крај сваког од производа завршава цифром којом множимо да бисмо добили тај производ!
Одређивање Броја Децималних Места
Сада треба израчунати збир свих појединачних производа како су смештени у запису. Почињемо са прорачуном са крајњом десном цифром. На крају је само број 6, па га само преносимо на дно. 5+4=9, ставимо 9. 3+0+2=6, ставимо 6. 1+9+5+8=23, ставимо 3 и запамтимо 2. 4+6 = 10 и два запамтимо 12, запишемо 2 и памтимо 1. 0 и један који памтимо, запишемо 1. На крају, само смо записали цифру 4 јер је сама.
Добили смо збир 4123596 и остаје да лоцирамо тачно место где треба ставити децимални зарез у самом производу. Први децимални број има две децимале, а други децимални број три децимале или оба децимала заједно имају укупно 5 децималних места. Зато рачунамо 5 места у производу с десна на лево и постављамо да има 5 децимала.
Производ децималних бројева 4,52 и 9,123 је 41,23596!
*Ако су у одређеној ситуацији последњих или последњих неколико цифара децималног броја које се налазе десно од децималног зареза 0, онда их слободно не пишете јер немају вредност!
Множење Децималних Бројева Скраћена Техника
Видео материјал који можете погледати кликом на видео испод омогућава вам да видите јединствену технику множења децималних бројева без праћења свих наведених корака класичног поступка множења децималних бројева. Искрено се надамо да ће вам се ова занимљива техника стенографије допасти и да ћете је увежбати приликом множења децималних бројева без калкулатора!
Горња техника вам омогућава да задивите своје родитеље, наставнике и друге одрасле својом способношћу да множите децимале на брз и лак начин без употребе калкулатора!
Tags: Бројева, Децималних, Множење, Пример

 Сачекајте...
Сачекајте...