Шта је линеарна једначина? Које методе се користе за одређивање тачног решења линеарне једначине? Како се у конкретном примеру из стварног живота може користити линеарна једначина за решавање проблема? Одговоре на претходна питања можете пронаћи на овој веб страници испод! Овде ћемо објаснити све што знамо о линеарној једначини, како направити линеарну једначину и како одредити њено решење! Испод на овој страници можете упоредити различите методе решавања линеарне једначине! У овом тексту ћемо се фокусирати на линеарну једначину са једном непознатом, ау будућности ћемо креирати посебан садржај за друге врсте линеарних једначина!
Шта Је Линеарна Једначина Са Једном Непознатом
Једначина дата на слици испод:
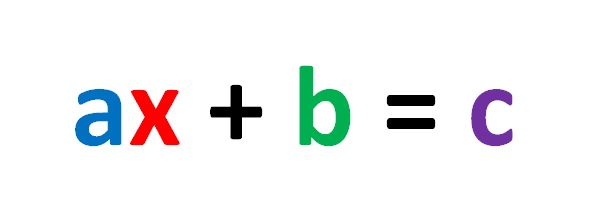
у којима су бројеви a, b и c реални бројеви и а није једнако нули, назива се линеарна једначина са једном непознатом!
Решење линеарне једначине је број који ћемо заменити на месту x и израчунати, добијамо тачну једначину!
Испод слике су три различите линеарне једначине са једном непознатом!
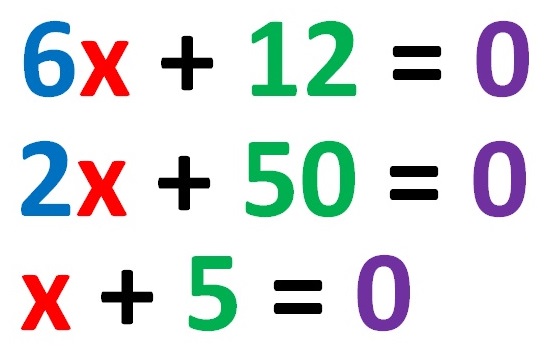
Решавање Линеарнa Једначинa
Хајде да покушамо да одредимо решење линеарне једначине! Погледајте пример у наставку!
Пример 1. Израчунајте решење линеарне једначине на слици испод!

Приликом решавања линеарне једначине циљ нам је да непознато x остане само на левој страни једначине, док све познате вредности пренесемо на десну страну једначине!
Да бисмо се решили -14 броја на левој страни, додаћемо +14 на обе стране једначине истовремено! Израз изгледа овако:
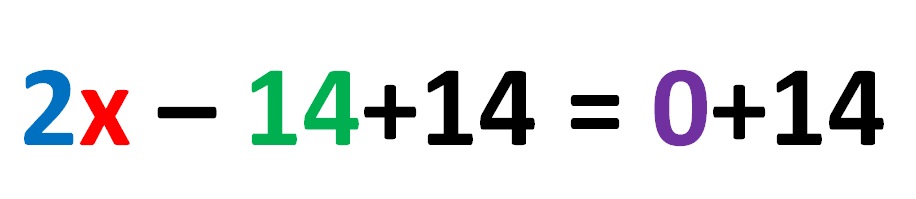
Након што израчунамо одговарајуће математичке операције и на левој и на десној страни линеарне једначине, добијамо:
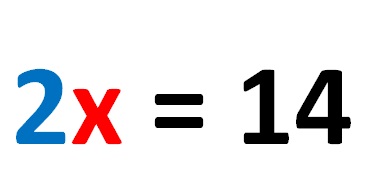
Број 2 који се још налази на левој страни линеарне једначине може да се уклони само ако се обе стране линеарне једначине поделе са бројем 2. Урадимо то! Израз има следећи облик:
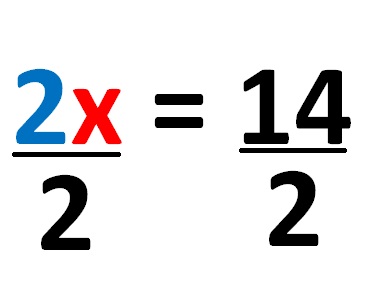
Након што обе стране линеарне једначине поделимо бројем 2, добијамо:
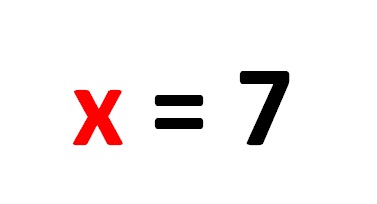
Више је него јасно да нам последњи корак нуди решење линеарне једначине, x=7!
Провера Решења Линеарнe Једначинe Са Једном Непознатом
Да бисмо се уверили да је решење које смо добили при решавању линеарне једначине реално, довољно је да добијено решење заменимо место x у линеарној једначини и израчунамо да ли ћемо добити тачну једначину.
Прво, заменимо резултујућу вредност уместо x у линеарној једначини!

Затим израчунавамо производ два броја, након чега се добија израз:

Пошто је 14-14=0 заиста тачна једначина, закључујемо да је број 7 заиста тачно решење линеарне једначине!
Креирање Линеарнa Једначина
Поред тачног решавања линеарне једначине са једном непознатом, веома је важно бити у стању да креирате линеарну једначину са једном непознатом у стварној ситуацији и решите одређени математички задатак! У наставку ћемо вам понудити конкретну ситуацију у којој можемо користити линеарну једначину као могуће решење за прави математички проблем!
Пример 2. Правоугаоник има обим од 40 метара! Дужина правоугаоника је 10 метара већа од његове ширине. Колика је дужина страница правоугаоника?
Наравно, за решавање таквог примера потребно је знати формулу за израчунавање обима правоугаоника! Кликните на обојени текст у претходној реченици да се сетите како да израчунате обим правоугаоника ако вам је потребан!
Од датих података о правоугаонику, прво треба да направимо слику која ће описати његове карактеристике! Слика може изгледати овако:
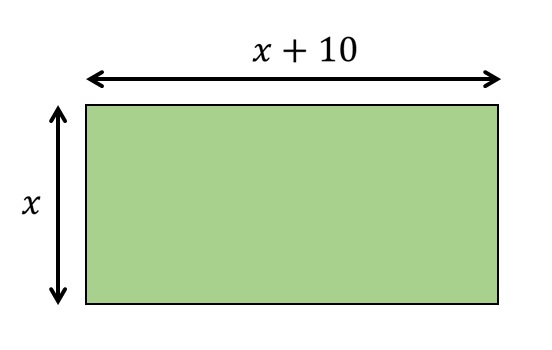
Доњи израз се добија применом правила за одређивање обима правоугаоника!

Прво ћемо на левој страни сакупити све појмове који садрже х, а посебно све оне који не садрже х. Истовремено ћемо унети 40 метара у место за вредност периметра! Израз има следећи облик:
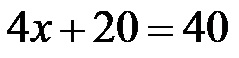
Одузимамо 20 са обе стране линеарне једначине, након чега једначина добија следећи облик:
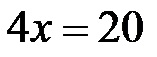
На крају, поделимо обе стране једначине бројем 4, након чега се добија коначно решење за дужину x!
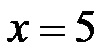
Коначно, треба да искористимо вредност x коју смо добили решавањем линеарне једначине да одредимо дужину страница правоугаоника! Ширина правоугаоника је 5 метара, док је његова дужина 15 метара, што задовољава услов да дужина буде 10 метара већа од ширине, а уједно и други услов да обим буде 40 метара!
Примери
Видео материјал на дну ове веб странице садржи огроман број решених примера линеарних једначина! Поред тога, видео ће вам сигурно помоћи да научите како да направите линеарну једначину у реалној ситуацији и да је користите за решавање математичког проблема! Предлажемо да погледате цео видео.

 Сачекајте...
Сачекајте...