Шта је квадратна једначина? Како се може одредити решење(а) квадратне једначине? Која је формула која се може користити за израчунавање решења квадратне једначине? У наставку овог места можете пронаћи тачне одговоре на ова питања. У наставку ћемо вам омогућити да видите потпуно решене примере у којима је решење одређене квадратне једначине практично.
Сваки наш читалац може да приступи видео материјалу који садржи огроман број решених примера који ће вам помоћи да трајно решите проблем квадратних једначина. Останите овде неколико минута да вам помогнемо да решите овај математички задатак.
Шта Је Квадратна Једначина
Једначина која има облик:
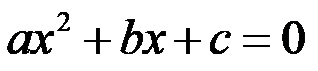
где је a различито од нуле, док су a, b и c реални коефицијенти назива се квадратна једначина!
Ако су сва три коефицијента различита од нуле онда кажемо да је квадратна једначина потпуна!
Ако је један од коефицијената b или c једнак нули (или су оба истовремено једнака нули), онда се за ту квадратну једначину каже да је непотпуна квадратна једначина.
Свака квадратна једначина може имати једно или два решења!
Формула за одређивање решењe или решења потпуне квадратне једначине је:
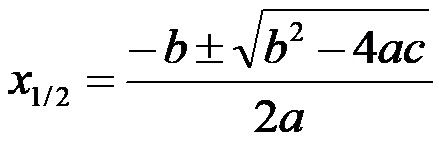
За одређивање решења треба користити три коефицијента. Лако се може направити грешка при лоцирању три коефицијента. Да би се избегле грешке, треба водити рачуна да ли је квадратна једначина у општем облику или не. Ако није у општем облику, прво треба да трансформишемо квадратну једначину у општи облик да бисмо тачно утврдили која је вредност три коефицијента.
Чим се детектују три коефицијента, њихова вредност се уноси у горњу формулу, након чега се одређују решења квадратне једначине.
У наставку можете видети како се израчунавају решења одређене квадратне једначине!
Како Одредити Решења Квадратне Једначине
Погледајте како су решења квадратне једначине одређена у примеру испод!
Пример 1. Одредити решења квадратне једначине дате на слици испод!
Квадратна једначина из горњег примера има коефицијенте a = 1, b = -3 и c= – 28! Ако се вредност ових коефицијената унесе у формулу за израчунавање, добија се следећи израз:
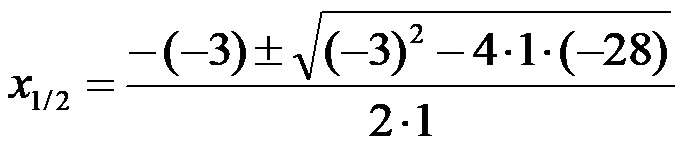
У следећем кораку израчунавамо квадрат унутар коренског израза и израчунавамо производ бројева испод коренског израза . Тада добијамо:
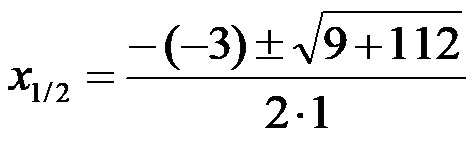
У следећем кораку сабираме испод корена и се ослобађамо двоструког минуса пре корена, након чега добијамо:
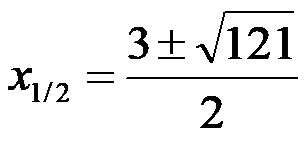
Сада, идемо на кореновање!
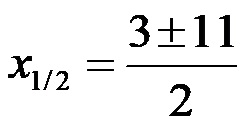
Коначно, при израчунавању првог решења уписује се знак +, а при израчунавању другог решења уписује се знак -. Формирање оба решења изгледа као на слици испод!
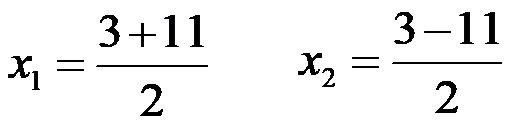
У бројиоцу првог решења сабирамо, док у бројиоцу другог решења одузимамо, након чега добијамо:
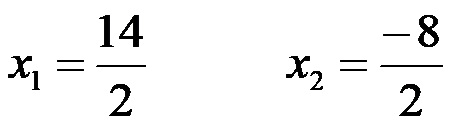
После дељења добијамо два решења 7 и -4!
Као што видите, одређивање решења квадратне једначине уопште није тежак математички поступак, али се због дужине решења мора пазити да се не направи мала грешка, која би могла да резултира погрешним решењима!
У овим математичким задацима увек је лепо проверити решења. Ако на местима к у квадратној једначини у две различите ситуације заменимо вредност решења и добијемо тачну једначину онда можемо бити уверени да смо квадратну једначину правилно решили.
Провера Решења
Хајде да проверимо да ли су два решења која смо добили помоћу формуле заиста тачна. Почећемо испитивањем првог решења, односно уместо x у квадратној једначини унећемо 7! Након уноса овог решења, израз добија следећи облик:
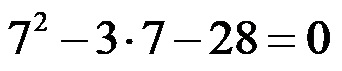
Настављамо са решавањем, где на почетку израчунавамо квадрат, након чега добијамо:
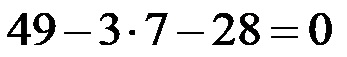
Затим израчунавамо производ!
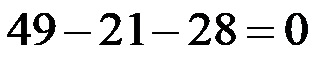
Коначно, сабирањем и одузимањем добијамо тачно решење (49-49=0)!
Исти поступак понављамо и са другим решењем. Сада на место x уносимо друго решење, односно број -4. Добијени израз је дат на слици испод!
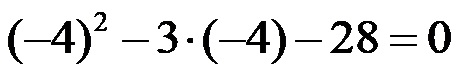
Понављамо поступак решавања који смо управо завршили за прво решење, па поново крећемо са квадрирањем.
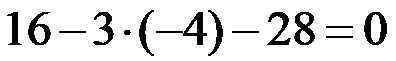
Израчунавамо производ.
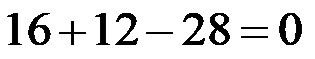
Сабирањем и одузимањем налазимо да је и друго решење тачно јер поново добијамо тачну једначину (28-28=0)!
На овај начин можемо са сигурношћу тврдити да су бројеви -4 и 7 заиста решења квадратне једначине! Препоручујемо вам да ову врсту провере извршите за сваки решени задатак, јер вам управо ова врста опреза може помоћи да једног дана пронађете сопствену грешку и да је на време исправите!
Видео Примери
Видео материјал у наставку садржи много информација о квадратној једначини и примерима у којима се израчунавају решења квадратне једначине. Користећи видео можете видети да врста решења или решења квадратне једначине зависи само од коренског израза или дискриминанта квадратне једначине!
У посебном водичу на нашој веб страници можете сазнати како да израчунате решења квадратне једначине која није потпуна!

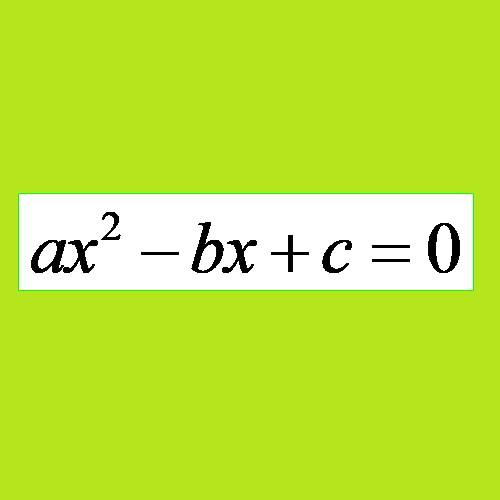
 Сачекајте...
Сачекајте...